В первой строке вынесем xy за скобки, а из второй выразим x+y:
Теперь подставим x+y из второго уравнения в первое:
Делаем замену вида :
Решим это уравнение:
Получили две сильно упрощенные системы:
или
Для первого случая:
Для второго случая:
Итого исходная система имеет четыре решения:
Система уравнений решена!
Вторая система уравнений:
Умножим первое уравнение на 5, а второе на 14:
Теперь приравняем левые части:
Выполним преобразования:
Теперь есть два подхода к решению:
Делим все уравнение на y², вводим замену вида и решаем уравнение . После чего получаем, что или . Дальнейшие действия очевидны.Разложим уравнение на множители, заметив, что .
Практикум написан на основе многолетнего опыта работы авто-
ра в классах с углубленным изучением физики и опыта подготовки
школьников к олимпиадам различного уровня. Задачник представляет
собой пособие, в котором рассмотрены и систематизированы основ-
ные приемы расчета электрических цепей. Применение каждого прие-
ма проиллюстрировано на примерах и сопровождается системой задач
для самостоятельного решения, как простых, так и повышенной слож-
ности и олимпиадных.
Практикум предназначен для поступающих в высшие учебные
заведения. Может быть использован в качестве учебного пособия в
классах с углубленным изучением физики лицеев и гимназий, а также
лицами, занимающимися самообразованием и подготовкой к олим-
пиадам.
(см. объяснение)
Объяснение:
Первая система уравнений:
Раскроем скобки:
В первой строке вынесем xy за скобки, а из второй выразим x+y:
Теперь подставим x+y из второго уравнения в первое:
Делаем замену вида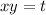 :
:
Решим это уравнение:
Получили две сильно упрощенные системы:
Для первого случая:
Для второго случая:
Итого исходная система имеет четыре решения:
Система уравнений решена!
Вторая система уравнений:
Умножим первое уравнение на 5, а второе на 14:
Теперь приравняем левые части:
Выполним преобразования:
Теперь есть два подхода к решению:
Делим все уравнение на y², вводим замену видаЯ рекомендую пользоваться первым .
Итак, имеем две системы:
Для первого случая:
Для второго случая:
Итого исходная система имеет четыре решения:
Система уравнений решена!
Задание выполнено!