1) Прямоугольник лежит на гипотенузе своей длинной стороной. Обозначим ее 5х, тогда короткая сторона прямоугольника будет 2х. Кусочки гипотенузы слева и справа от стороны прямоугольника будут тоже по 2х,т.к. отсеченные слева и справа части треугольника являются равнобедренными прямоугольными треугольниками. Следовательно длина гипотенузы исходного треугольника будет 5х+2х+2х=9х=45, отсюда х=5. Значит, длинная сторона прямоугольника 5х=25, а короткая 2х=10; 2) Прямоугольник лежит а гипотенузе своей короткой стороной. Обозначим ее 2х, тогда длинная будет 5х. Как и в предыдущем случае отсеченные слева и справа треугольники будут прямоугольными равнобедренными, т.е. оба их катета будут 5х. Тогда гипотенуза будет 5х+5х+2х=12х=45, отсюда х=3,75. Тогда длинная сторона прямоугольника 5х=5*3,75=18,75, а короткая 2х=2*3,75=7,5
Угол А будет равен арксинусу этого числа 59,95 можно округлить до 60°.
5) В треугольнике угол MNO будет равен 30°, поскольку в треугольник MNK прямоугольный. Гипотенуза MN будет равно 6, так как катет МО лежит на против угла в 30°, а значит он равен половине гипотенузы. Катет NO находим по теореме Пифагора . В прямоугольном треугольнике NOK катет NO лежит на против угла в 30°, значит он равен половине гипотенузы, следовательно гипотенуза NK = 10,4. Катет ОК находим по теореме Пифагора ОК = 9,0066 округлим до 9. МК = МО + ОК = 12.
2 Вариант
1) Сумма всех углов прямоугольного треугольника равна 180°, следовательно угол К будет равен К = 180 - 90 - 72 = 18°.
2) Катет ВС лежит на против угла А, который равен 30°, следовательно катет равен половине гипотенузы 15 см.
3) Катет XZ лежит на против угла в 30° он равен половине гипотенузы, следовательно гипотенуза XY = 2*XZ = 24.
4) Находим катет АС по теореме Пифагора. АС = 36,4. Находим синус угла В, sin(B) = 36,4/42 = 0,8666. Угол В будет равен арксинусу этого числа. Угол В равен 60,07° можно округлить до 60°
5) В прямоугольном треугольнике АВС, катет АС лежит на против угла в 30°, следовательно он равен половине гипотенузы АВ, катет АС = 40 см. В треугольнике МСВ угол МСВ равен 60°, поскольку в этом треугольнике угол СМВ прямой. Следовательно угол АСМ = 90-60 = 30°. В треугольнике АСМ катет АМ лежит на против угла в 30° и он равен половине от гипотенузы АС, следовательно катет АМ = 20см.
2) Прямоугольник лежит а гипотенузе своей короткой стороной. Обозначим ее 2х, тогда длинная будет 5х. Как и в предыдущем случае отсеченные слева и справа треугольники будут прямоугольными равнобедренными, т.е. оба их катета будут 5х. Тогда гипотенуза будет 5х+5х+2х=12х=45, отсюда х=3,75. Тогда длинная сторона прямоугольника 5х=5*3,75=18,75, а короткая 2х=2*3,75=7,5
1 вариант
1) Сумма всех углов прямоугольного треугольника 180°, следовательно угол А = 180-90-43 = 47°
2) Катет лежащий на против угла в 30° градусов равен половине гипотенузы СВ = АВ/2 = 12см
3) Катет лежащий на против угла в 30° градусов равен половине гипотенузы угол М = 30°, следовательно KL = КМ/2 = 9 см
4) Находим катет ВС по теореме Пифагора
Находим синус угла А, sin(A) = 13,85/16 = 0,865625
Угол А будет равен арксинусу этого числа 59,95 можно округлить до 60°.
5) В треугольнике угол MNO будет равен 30°, поскольку в треугольник MNK прямоугольный. Гипотенуза MN будет равно 6, так как катет МО лежит на против угла в 30°, а значит он равен половине гипотенузы. Катет NO находим по теореме Пифагора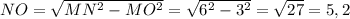
. В прямоугольном треугольнике NOK катет NO лежит на против угла в 30°, значит он равен половине гипотенузы, следовательно гипотенуза NK = 10,4. Катет ОК находим по теореме Пифагора ОК = 9,0066 округлим до 9. МК = МО + ОК = 12.
2 Вариант
1) Сумма всех углов прямоугольного треугольника равна 180°, следовательно угол К будет равен К = 180 - 90 - 72 = 18°.
2) Катет ВС лежит на против угла А, который равен 30°, следовательно катет равен половине гипотенузы 15 см.
3) Катет XZ лежит на против угла в 30° он равен половине гипотенузы, следовательно гипотенуза XY = 2*XZ = 24.
4) Находим катет АС по теореме Пифагора. АС = 36,4. Находим синус угла В, sin(B) = 36,4/42 = 0,8666. Угол В будет равен арксинусу этого числа. Угол В равен 60,07° можно округлить до 60°
5) В прямоугольном треугольнике АВС, катет АС лежит на против угла в 30°, следовательно он равен половине гипотенузы АВ, катет АС = 40 см. В треугольнике МСВ угол МСВ равен 60°, поскольку в этом треугольнике угол СМВ прямой. Следовательно угол АСМ = 90-60 = 30°. В треугольнике АСМ катет АМ лежит на против угла в 30° и он равен половине от гипотенузы АС, следовательно катет АМ = 20см.