Катет прямоугольного треугольника равен 20 см , гипотенуза - 25 см , а периметр больше катета в три раза. Определите его площадь

1. Касательные проведнные с одной точки равны между собой, поэтому

AC = AB = 12 см.

По теореме Пифагора

AO=корень(CO^+AC^2)=корень(9^2+12^2)=15 см

ответ: 12 см, 15 см

2. Извини, но незнаю

3. Хорды MN и PK пересекаются в точке E так, что ME = 12 см, NE = 3 см, PE = KE. Найдите PK.

По свойству хорд

ME*NE=PE*KE

Пусть PE = KE=х см

Тогда x^2=12*3=36

x>0, поєтому х=6 см

PK=PE+KE=6см+6см=12 см

ответ:12 см

4.Треугольник ОАВ равнобедренный, ОА=ОВ=16 см (радиусы);

∠А=∠В=30° - по условию;

ОН - высота ОАВ, равна 16/2=8 см (катет против угла 30°);

АВ=2*АН=2*√(16²-8²)=16√3 см.

Треугольник СОВ равнобедренный, ОС=ОВ=16 см (радиусы);

∠С=∠В=45° ⇒ ∠О=90° - прямоугольный ⇒ СВ=√(16²+16²)=16√2 см.

АВ=16√3 см;

ВС=16√2 см.

11.

Дано:

ΔАВС - равнобедренный

АС = ВС = 13

АВ = 10

Найти:

АС - высоту. опущенную на боковую сторону

СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.

По теореме Пифагора

АС² = CD² + AD²

13² = CD² + 5²

CD² = 13² - 5² = 144 = 12²

CD = 12

Площадь треугольника АВС

S = 0.5 CD · AB = 0.5 · 12 · 10 = 60

Площадь треугольника АВС можно также вычислить и так:

S = 0.5 BC · AE

откуда

АЕ = 2S : BC = 2 · 60 : 13 = 9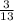 ≈ 9.23

АЕ = 9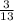 ≈ 9.23

12.

Дано:

MKNR - ромб

KR = 10 - 1-я диагональ ромба

MN = 12 - 2-я диагональ ромба

Найти:

МК - сторону ромба

Пусть О - точка пересечения диагоналей ромба.

Диагонали ромба делятся точкой пересечения пополам, поэтому

КО = 0,5 KR = 0.5 · 10 = 5

МО = 0,5 MN = 0.5 · 12 = 6

Диагонали ромба пересекаются под прямым углом, поэтому

КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.

По теореме Пифагора

МК² = КО² + МО²

МК² = 5² + 6² = 61

МК = √61 ≈ 7,81

Сторона ромба МК =√61 ≈ 7,81