Контрольна робота
Геометричні перетворення
1. Знайдіть координати точок, симетричних точкам N(–3;–1) і M(5;0)
відносно: a) осі ординат; b) осі абсцис; c) початку координат.
2. Накресліть трикутник ABC. Побудуйте образ трикутника ABC: a) при
симетрії відносно точки N, яка є серединою сторони BC; b) при симетрії
відносно прямої AC; c) при гомотетії з центром в точці A і коефіцієнтом
k = – 2.
3.Сторони двох правильних шестикутників відносяться як 3 : 5, а площа
меншого з них дорівнює 72см2 . Знайдіть площу більшого шестикутника.
4. При паралельному перенесенні образом точки A(4;–2) є точка B(–1;7). Яка
точка є образом точки N(0;–4) при цьому паралельному перенесенні ?
5. Скласти рівняння фігури, яка симетрична колу (�� + 4) 2 + (�� – 2) 2 = 6
відносно: a) осі ординат; b) осі абсцис; c) початку координат.
6. Квадрат зі стороною 6 см повернули навколо його центра на кут 45°.
Знайдіть периметр восьмикутника, що утворився.
7. Сторони трикутника дорівнюють 10 см, 17 см і 24 см. Бісектрису
трикутника, проведену з вершини його меншого кута, поділено у відношенні
2 : 5, рахуючи від вершини, і через точку поділу проведено пряму,
паралельну меншій стороні. Знайдіть площу отриманої при цьому трапеції.
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.
Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.
BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: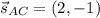 .
.
Точка А(5,-3)∈АС и уравнение АС имеет вид:
CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: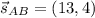 .
.
Точка А(5,-3)∈АВ и уравнение АВ имеет вид:
Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .
d(М, АВ) = d(M, BC) = 4 дм
d(M, AD) = d(M, СD) = 2√5 дм
d(M, BD) = 4 дм
d(M, AC) = 3√2 дм
Объяснение:
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к этой прямой.
МВ - перпендикуляр к плоскости квадрата, а значит, и к любой прямой, лежащей в этой плоскости.
МВ⊥АВ, значит расстояние от точки М до прямой АВ
d(М, АВ) = МВ = 4 дм
МВ⊥ВС, значит
d(M, BC) = MB = 4 дм
МВ⊥BD, значит
d(M, BD) = MB = 4 дм
BA⊥AD как стороны квадрата,
ВА - проекция МА на плоскость, значит МА⊥AD по теореме о трех перпендикулярах, тогда
d(M, AD) = MA
Аналогично, ВС⊥CD как стороны квадрата, ВС - проекция МС на плоскость, значит МС⊥CD по теореме о трех перпендикулярах, тогда
d(M, СD) = MС
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные:
ВС = ВА (стороны квадрата), значит МС = МА.
Из прямоугольного треугольника АВМ по теореме Пифагора:
МА = √(АВ² + ВМ²) = √(4 + 16) = √20 = 2√5 дм
Итак,
d(M, AD) = d(M, СD) = 2√5 дм
Осталось найти расстояние от М до диагонали АС.
ВО⊥АС по свойству диагоналей квадрата,
ВО - проекция МО на плоскость квадрата, значит
МО⊥АС по теореме о трех перпендикулярах.
d(M, AC) = MO
BD = AB√2 =2√2 дм как диагональ квадрата,
BО = BD/2 = √2 дм (диагонали квадрата делятся точкой пересечения пополам)
Из прямоугольного треугольника МВО по теореме Пифагора:
МО = √(ВО² + ВМ²) = √(2 + 16) = √18 = 3√2 дм
d(M, AC) = 3√2 дм