Кожна бічна грань чотирикутної піраміди, в основі якої лежить квадрат,
нахилена до основи під кутом 60° · Площа основи піраміди 16 см2
. Знайдіть висоту піраміди.

Любое осевое сечение усеченного конуса - это равнобедренная трапеция (причем одна и та же, конус - фигура вращения), а осевое сечение сферы (и вообще любое сечение сферы) - это окружность. 

Если можно вписать сферу в конус, значит в любое осевое сечение можно вписать окружность. А в описанной равнобедренной трапеции боковая сторона равна полусумме оснований. И наоборот, если равна - то можно вписать.

Отсюда следует и утверждение задачи.

Вообще,  базовое утверждение касается описанных выпуклых четырехугольников - у них суммы противоположных сторон равны. И наоборот - если равны, то можно вписать окружность.

                                                                Дано: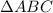 

                                                                угол А = 48

                                                                угол В = 44

                                                                АD, BE, CF - биссектрисы пересекающиеся = О

                                                              _________________________

                                                            АОF - ?

                                                   Решение.

1) Т.к сумма углов треугольника равна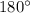  (по теореме о сумме углов в треугольнике), то угол С =  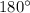- угол А - угол В = 

2) Т.к биссектриса делит угол пополам (по определению биссектрисы), то углы ЕВА и ЕВС =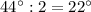 ; углы FCA и FCB = 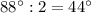; углы DAC и DAB = .

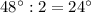3) Т.к сумма углов треугольника равна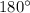  (по теореме о сумме углов в треугольнике), то угол АОС =  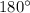- угол ОАС - угол ОСА = . 

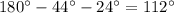4) Т.к сумма смежных углов равна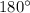  (по теореме о смежных углах), то угол AOF =  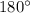- угол АОС =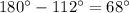

ответ: угол AOF = 68 градусов.