2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
Где (a;b) координаты центра окружности.
В данном уравнении
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.
1)Раз АВ = 7, то и СD = 7, диагонали в точке пересечения делятся пополам. В итоге: АО = 3, ВО = 5, АВ = 7. ответ: 3+5+7=15 см
2)Площадь трапеции вычисляется по формуле: (ВС+АД)/2×ВН. на рисунке изображена равнобедренная трапеция: АВ=СД=4. Проведём из вершин В и С две высоты к нижнему основанию АД: ВН и СК. Они делят АД так что ВС=НК=5, а АН=КД. Рассмотрим полученный ∆АВН. Он прямоугольный и в нём АН и ВН- катеты, а АВ - гипотенуза. <А=60°, а сумма острых углов прямоугольного треугольника составляет 90°, поэтому <АВН=90–60=30°. Катет АН, лежащий напротив угла 30° равен половине гипотенузы, поэтому АН=АВ÷2=4÷2=2.
Теперь найдём ВН по теореме Пифагора:
ВН ²=АВ²–АН²=4²–2²=16–4=12; ВН=СК=√12=2√3
Если АН=КД=2, а НК=5, тогда
АД=2×2+5=4+5=9.
Теперь найдём площадь трапеции зная её высоту и оба основания:
смотри ниже
Объяснение:
2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
Где (a;b) координаты центра окружности.
В данном уравнении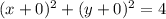
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.
1)Раз АВ = 7, то и СD = 7, диагонали в точке пересечения делятся пополам. В итоге: АО = 3, ВО = 5, АВ = 7. ответ: 3+5+7=15 см
2)Площадь трапеции вычисляется по формуле: (ВС+АД)/2×ВН. на рисунке изображена равнобедренная трапеция: АВ=СД=4. Проведём из вершин В и С две высоты к нижнему основанию АД: ВН и СК. Они делят АД так что ВС=НК=5, а АН=КД. Рассмотрим полученный ∆АВН. Он прямоугольный и в нём АН и ВН- катеты, а АВ - гипотенуза. <А=60°, а сумма острых углов прямоугольного треугольника составляет 90°, поэтому <АВН=90–60=30°. Катет АН, лежащий напротив угла 30° равен половине гипотенузы, поэтому АН=АВ÷2=4÷2=2.
Теперь найдём ВН по теореме Пифагора:
ВН ²=АВ²–АН²=4²–2²=16–4=12; ВН=СК=√12=2√3
Если АН=КД=2, а НК=5, тогда
АД=2×2+5=4+5=9.
Теперь найдём площадь трапеции зная её высоту и оба основания:
S=(5+9)/2×2√3=14÷2×2√3=14√3
Объяснение:
я не умею но решение по теме