Условие: Треугольники АВС и А₁В₁С₁ подобны, причем сторонам BC и АС соответствуют стороны B₁C₁ и А₁С₁. Найдите неизвестные стороны этих треугольников, если АC=28 см, АB=49 см, В₁С₁=24 см, А₁С₁=16 см.
Дано:
ΔАВС подобен ΔА₁В₁С₁, АC=28 см, АB=49 см, В₁С₁=24 см, А₁С₁=16 см.
Найти: ВС, А₁В₁.
Так как по условию треугольники АВС и А₁В₁С₁ подобны, то можем составить отношения сходственных сторон:
Дано: А(-3; 9), В(-4; -8), С(6; 0)
Найти:
а)координаты вектора АС;
б)длину вектора ВС;
в)координаты середины отрезка АВ:
г)периметр треугольника АВС;
д)длину медианы СМ.
a) AC = {Cx - Ax ; Cy - Ay}
AC = {6 - (-3) ; 0 - 9}
AC ={9 ; -9}
б) BC = {Cx - Bx ; Cy - By}
BC = {6 - (-4); 0 - (-8)}
BC = {10 ; 8}
|BC| =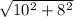 =
= 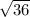 = 6
= 6
в) Пусть это будет точка M, тогда её координаты будут равны
M((Ax + Bx)/2 ; (Ay + By)/2)
M((-3 + -4)/2 ; (9 + 8)/2)
M(-3,5 ; 8,5)
г) Посчитаем длину каждой стороны треугольника
AB =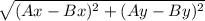 =
= 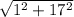 =
= 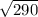
AC =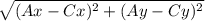 =
= 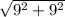 =
= 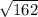
д) СМ =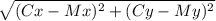 =
= 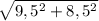 =
= 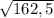
Условие: Треугольники АВС и А₁В₁С₁ подобны, причем сторонам BC и АС соответствуют стороны B₁C₁ и А₁С₁. Найдите неизвестные стороны этих треугольников, если АC=28 см, АB=49 см, В₁С₁=24 см, А₁С₁=16 см.
Дано:
ΔАВС подобен ΔА₁В₁С₁, АC=28 см, АB=49 см, В₁С₁=24 см, А₁С₁=16 см.
Найти: ВС, А₁В₁.
Так как по условию треугольники АВС и А₁В₁С₁ подобны, то можем составить отношения сходственных сторон:
AB/A₁B₁ = BC/B₁C₁ = AC/A₁C₁
1. BC/B₁C₁ = AC/A₁C₁
BС = (AC/A₁C₁) * B₁C₁ = (28/16) * 24 = (7/4) * 24 = 42 см
2. AB/A₁B₁ = BC/B₁C₁
A₁B₁ = (В₁C₁/ВC) * AB = (24/42) * 49 = (4/7) * 49 = 28 см
ответ: BC=42 см, A₁B₁=28 см.