Кулю, радіус якої дорівнює 20 см, перетнути площиною. Площа утвореного перерізу дорівнює 144 п см2

Пусть стороны АВ и ВС треугольника соответственно равны 1 и √15 а его медиана ВМ равна 2.На продолжении медианы BM за точку M отложим отрезок MD, равный BM. Из равенства треугольников ABM и CDM (по двум сторонам и углу между ними) следует равенство площадей треугольников ABC и BCD. В треугольнике BCD известно, что
ВС=√15; ВD=2ВМ = 2*2=4 ; DС=АВ=1
по формуле герона
р=(√15+4+1)/2=(√15+5)/2
s=√(p(p-BC)(p-BD)(p-DC))=√((√15+5)/2)((√15+5)/2-√15)((√15+5)/2-4)((√15+5)/2-1)=
√((√15+5)/2)((-√15+5)/2)((√15-3)/2)((√15+3)/2)=√(((√15+5)(5-√15)(√15-3)(√15+3))/16)
=√(((25-15)(15-9))/16)=√60/√16=2√15/4
2*3.87/4=1.94

На рисунке изображен график линейной функции. Напишите формулу, которая задает линейную функцию

. Уравнение прямой в отрезках

Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид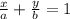     где a и b - некоторые отличные от нуля действительные числа , при чем | a| и |b| равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат.

. Через координаты 2-х точек.

Уравнение прямой у=кх+в.

Точка пересечения с Оу имеет координаты ( 0; 4)⇒ 4= к*0+в ,в=4

Точка пересечения с Ох имеет координаты (-4; 0) ⇒  0=к*(-4)+в или

0=-4к+4 , к=1.

Уравнение прямой у=х+4.