Пусть диагонали ромба пересекаются в точке О: АС ∩ ВD = О, диагонали ромба относятся как 3:4 ⇒ половины диагоналей ромба также относятся как 3:4 ⇒ можно обозначить: АО = 4х, ОВ = 3х. Периметр ромба равен 40 ⇒ его сторона равна 40 : 4 = 10,
АВ = ВС = СD = DА = 10. По теореме Пифагора:
АВ² = АО² + ВО² = = 10² = 100 ⇒
x² = 100 : 25 = 4 ⇒ x = 2 ⇒ АО = 4х = 4*2 = 8, ОВ = 3х = 3*2 = 6,
AC = 2AO = 2*8 = 16, ВD = 2ОВ = 2*6 = 12. Площадь ромба равна:
S = 0,5 * AC * ВD = BH * AD ⇒
ответ: высота ромба ВН равна 9,6
Объяснение:
2 ) | b | = 28 ; вектор а{- 6 ; 4 ; 12 } ; a⇅b ;
нехай коорд . вектора b{ x ; y ; z } , тоді | b | = √( x² + y² + z² ) = 28 ;
x² + y² + z² = 784 .
Вектори а і b - колінеарні , тому x/(- 6 ) = y/4 = z /12 = λ . Звідси
x = - 6λ ; y = 4λ ; z = 12λ . Підставляємо значення :
(- 6λ )² + ( 4λ )² + ( 12λ )² = 784 ;
196λ² = 784 ;
λ² = 784 : 196 ;
λ² = 4 ;
λ = ± 2 ; 1) λ = - 2 ; x = - 6*(-2) =12 ; y = 4*(-2) = - 8 ; z = 12*(-2) = - 24 ;
2) λ = 2 ; x = - 6*2 = - 12 ; y = 4*2 = 8 ; z = 12 *2 = 24 .
В - дь : є два розв"язки : 1) b{ 12 ;- 8 ;- 24 } i 2) b{- 12 ; 8 ; 24 } .
Пусть диагонали ромба пересекаются в точке О: АС ∩ ВD = О, диагонали ромба относятся как 3:4 ⇒ половины диагоналей ромба также относятся как 3:4 ⇒ можно обозначить: АО = 4х, ОВ = 3х. Периметр ромба равен 40 ⇒ его сторона равна 40 : 4 = 10,
АВ = ВС = СD = DА = 10. По теореме Пифагора:
АВ² = АО² + ВО² =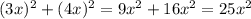 = 10² = 100 ⇒
= 10² = 100 ⇒
x² = 100 : 25 = 4 ⇒ x = 2 ⇒ АО = 4х = 4*2 = 8, ОВ = 3х = 3*2 = 6,
AC = 2AO = 2*8 = 16, ВD = 2ОВ = 2*6 = 12. Площадь ромба равна:
S = 0,5 * AC * ВD = BH * AD ⇒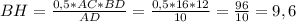
ответ: высота ромба ВН равна 9,6
Объяснение:
2 ) | b | = 28 ; вектор а{- 6 ; 4 ; 12 } ; a⇅b ;
нехай коорд . вектора b{ x ; y ; z } , тоді | b | = √( x² + y² + z² ) = 28 ;
x² + y² + z² = 784 .
Вектори а і b - колінеарні , тому x/(- 6 ) = y/4 = z /12 = λ . Звідси
x = - 6λ ; y = 4λ ; z = 12λ . Підставляємо значення :
(- 6λ )² + ( 4λ )² + ( 12λ )² = 784 ;
196λ² = 784 ;
λ² = 784 : 196 ;
λ² = 4 ;
λ = ± 2 ; 1) λ = - 2 ; x = - 6*(-2) =12 ; y = 4*(-2) = - 8 ; z = 12*(-2) = - 24 ;
2) λ = 2 ; x = - 6*2 = - 12 ; y = 4*2 = 8 ; z = 12 *2 = 24 .
В - дь : є два розв"язки : 1) b{ 12 ;- 8 ;- 24 } i 2) b{- 12 ; 8 ; 24 } .