Линия ABC параллельна линии DEF. Если BG перпендикулярен CE, если AD параллелен BG, если GF перпендикулярен EF, если BG=4m, GC=3m и AD=12м. Найдите a) длину BC, б) площадь треугольника ABD и в) длина GF.

Сумма односторонних углов равна 180°

1. 180°-118°=62°

2.180°-64=116°

3. Сумма внешнего угла с углом, по отношению к которому он является внешним, равна 180°. 180°-62°=118°. У параллелограмма 2 острых и 2 тупых угла, так 118° - больший угол, что нам и нужно.

4.

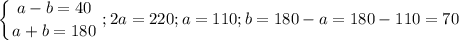
Это угол 70°

5. Наверное, сумма всех тупых углов параллелограмма.

Они равны, каждый равен 260°/2=130°, острые углы равны 180°-130°=50°

6.

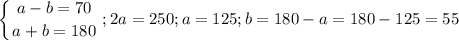
Это 55°

7.

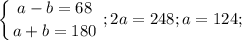
Это 124°

8.

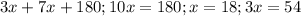
Это 54°

9. Диагональ делит параллелограмм на 2 равных треугольника. При этом 2 угла в нем известны, а третий как раз угол параллелограмма (тупой). 180°-(26°+34°)=180°-60°=120°.

Меньший угол 180°-120°=60°

10. Высота отсечет прямоугольный треугольник с одним известным острым углом 28°, второй равен 90°-28°=62°, это острый угол параллелограмма. Тупой равен 180°-62°=118°

1. Острый в сумме с тупым составляют 180°, т.к. прилежат к одной стороне. Поэтому 180°-118°=62°

2. 180°-64°=116°

3. Внутренний, смежный с данным, равен 180°-62°=118°, он и будет большим, т.к. два других острые.

4. Разность х-у=40, а их сумма по свойству х+у=180, поэтому 2х=220, тогда х=110, а у=180°-110°=70°- меньший из углов параллелограмма.

5. 360°-260°=100°, т.к. сумма всех четырех углов равна 360°.

6. Пусть меньший   угол х, х+х+70=180; 2х=110, тогда х=55°

7. Пусть больший угол х, х+х-68=180, 2х=248, х=124°

8. коэффициент пропорциональности х, тогда 3х+7х=180, откуда х=18, тода меньший угол равен 3*18°=

9. Диагональ разбивает параллелограмм на два равных треугольника, сумма углов которых равна 180°, значит, один угол у параллелограмма равен 180°-26°-34°=120°,  тогда другой  равен 180°-120°=60°

10. высота отсекает треугольник с углами 90°; 28°, и третьим углом, который является и углом параллелограмма и равен

180°-90°-28°=62°.  Значит, второй  угол равен 180°-62°=118°