Луч АЕ биссектриса угла А на сторонах угла отложены равные отрезки АК и АМ. запишите равные элементы треугольников АКЕ АМЕ и определите, по какому признаку треугольники равны
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б)
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
Могут, при условии, что В и С лежат в одной плоскости. 1. прямые А и В пересекаются, значит они лежат в одной плоскости и не являются параллельными. 2. прямая С скрещивается с прямой А - значит они не лежат в одной плоскости, и не являются параллельными. 3. Определение плоскости: плоскость задается либо двумя пересекающимися, либо двуми параллельными прямыми. 4. Раз прямая С не принадлежит плоскости прямых А и В, то она может задать плоскость прямых С и В. НО! МОЖЕТ, а не обязательно создаст, и МОЖЕТ быть паралльеной прямой В, но не обязательно параллельна.
1. Могут.
2. б) 6 см
3. б) 45°
Объяснение:
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б)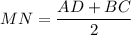
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
а) ВС лежит в плоскости (АВС),
МА пересекает (АВС) в точке А,
А не лежит на прямой ВС, значит
МА и ВС скрещивающиеся.
б) ∠(МА, AD) = 45° по условию,
BC║AD, значит
∠(МА, ВС) = 45°
1. прямые А и В пересекаются, значит они лежат в одной плоскости и не являются параллельными.
2. прямая С скрещивается с прямой А - значит они не лежат в одной плоскости, и не являются параллельными.
3. Определение плоскости: плоскость задается либо двумя пересекающимися, либо двуми параллельными прямыми.
4. Раз прямая С не принадлежит плоскости прямых А и В, то она может задать плоскость прямых С и В. НО! МОЖЕТ, а не обязательно создаст, и МОЖЕТ быть паралльеной прямой В, но не обязательно параллельна.