люди мне .. Хоть одно задания ...
1.Дано х=2m+n,y=m-3n . Выразить через m и векторы
а)2х-3у; б)3х+1/3у
2.В треугольнике абс:ва=в и са=а,вв1-медиана. Выразить вв1 через векторы а и в

Показать ответ

Ответ:

sddnblck

30.04.2022 19:42

Задача 1

Решение(согласно моему рисунку)

1) Проведем высоту ВН.

2) Рассмотрим четырехугольник АВНД

Он будет параллелограммом, т.к. АВ || СД (как основания), а АД || ВН (т.к. высоты к одной стороне)

Тогда, т.к. АВНД - параллелограмм, АВ=ДН=6 см., АД=ВН (по св-ву параллелограмма)

3) Рассмотрим прямоугольный треугольника ВНС

НС=10 - 6=4 см.

Угол С=60° (по условию)

Тогда угол НВС=90° - 60°=30°.

В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы. Гипотенуза ВС=8 см. (это и будет большая боковая сторона)

ВС²=ВН² + НС² (теорема Пифагора)

ВН²=64 - 16

ВН²=48

ВН=4√3

4) ВН=АД=4√3, тогда АД=4√3 (это и будет меньшая боковая сторона)

ответ: АД=4√3 см., ВС=8 см.

0,0(0 оценок)

Ответ:

drug20082005Ира

16.11.2020 23:01

Основанием пирамиды является равнобедренный треугольник с углом α при основании и радиусом вписанной окружности г. Две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания, а третья - наклонена к ней под углом β. Найдите объём пирамиды.

Объяснение: V(пир.)=1/3*S(основания)*h , h- высота пирамиды.

1) Найдем S(основания)=S(ΔАВС)=1/2*АС*ВН=АН*ВН.

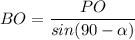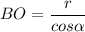Из ΔАВН ,угол ∠АВН=90°-α. По свойству касательной ОР⊥АВ, ОР=r ,Тогда из ΔВРО-прямоугольного $\displaystyle BO=\frac{PO}{sin(90-\alpha )}$ или $\displaystyle BO=\frac{r}{cos \alpha }$ .

Высота ВН=ВО+ОН ,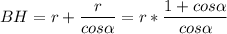 $\displaystyle BH=r+\frac{r}{cos \alpha }=r*\frac{1+cos\alpha }{cos\alpha }$ .

Из ΔАОН ,найдем АН. Тк АО-биссектриса , то ∠ОАН=α/2 ⇒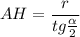 $\displaystyle AH=\frac{r }{tg\frac{\alpha }{2} }$ .

S(ΔАВС)=АН*ВН= $\displaystyle \frac{r }{tg\frac{\alpha }{2} }*r*\frac{1+cos\alpha }{cos\alpha }=\frac{r^{2} *(1+cos\alpha )}{cos\alpha *tg\frac{\alpha }{2} }$ .

2) Т.к две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания , то линия пересечения , отрезок МВ⊥(АВС)⇒ МВ-высота пирамиды..

Т.к ВН⊥АС , то и наклонная МН⊥АС по т. о трех перпендикулярах.Тогда углом между плоскостями (АВС) и ((АМС) будет линейный угол ∠ВНМ=β.

ΔМВН-прямоугольный , $\displaystyle tg\beta =\frac{BM}{BH}$ ,

$\displaystyle BM=BH* tg\beta =r*\frac{1+cos\alpha }{cos\alpha } *tg\beta$ , $\displaystyle BM=\frac{r*tg\beta *(1+cos\alpha) }{cos\alpha }$ .

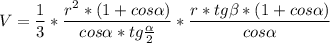3)Обьем $\displaystyle V= \frac{1}{3}* \frac{r^{2} *(1+cos\alpha )}{cos\alpha *tg\frac{\alpha }{2} } *\frac{r*tg\beta *(1+cos\alpha) }{cos\alpha }\\$ ,