Т.к. все три точки сечения призмы лежат попарно в одних и тех же плоскостях, то сечение строится попарным соединением точек - получаем в сечении ΔAB1C
Т.к. четырехугольники AA1B1B и BB1C1C равны, то равны и их диагонали AB1 и B1C ⇒ ΔAB1C равнобедренный.
Проведем медиану B1O в ΔAB1C, одновременно она будет и высотой ⇒ B1O ⊥ AC
Проведем медиану BO в равнобедренном ΔABC, одновременно она будет и высотой ⇒ BO ⊥ AC
Значит BOB1 будет углом между плоскостью сечения и нижним основанием, а т.к. нижнее и верхнее основание параллельны, то он равен углу между плоскостью сечения и верхним основанием, т.е. 45°
Из ΔBOB1, зная, что BO равно половине диагонали квадрата, найдем, что высота призмы BB1 = d /2
Из прямоугольного равнобедренного ΔABC с гипотенузой AC = d, найдем
Объем призмы найдем как произведение площади основания на высоту:
Медианы треугольника перечеркаются в отношении 2:1 тогда все медиана относится к точке сечения как 1:3 обозначим p основание одной из медиан тогда по правилу параллелограмма (p основание медианы на ab) op=oa+ob векторы надеюсь понятно почему тк если треугольник до строить до параллелограмма тк диагонали параллелограмма перечеркаются и точкой пересечения делятся пополам ) теперь по правилу треугольника запишем op+pc =мс и еще что om+op=mp мы знаем что pm=1/3 pc тогда тк op=ao+ob то PC=ao+ob+oc тогда по теореме деления отрезка в данном отношении oc/om=3:1 отсюда om=1/3(oa+ob+oc)
Т.к. все три точки сечения призмы лежат попарно в одних и тех же плоскостях, то сечение строится попарным соединением точек - получаем в сечении ΔAB1C
Т.к. четырехугольники AA1B1B и BB1C1C равны, то равны и их диагонали AB1 и B1C ⇒ ΔAB1C равнобедренный.
Проведем медиану B1O в ΔAB1C, одновременно она будет и высотой ⇒ B1O ⊥ AC
Проведем медиану BO в равнобедренном ΔABC, одновременно она будет и высотой ⇒ BO ⊥ AC
Значит BOB1 будет углом между плоскостью сечения и нижним основанием, а т.к. нижнее и верхнее основание параллельны, то он равен углу между плоскостью сечения и верхним основанием, т.е. 45°
Из ΔBOB1, зная, что BO равно половине диагонали квадрата, найдем, что высота призмы BB1 = d /2
Из прямоугольного равнобедренного ΔABC с гипотенузой AC = d, найдем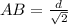
Объем призмы найдем как произведение площади основания на высоту: