Между сторонами угла АОВ, равного 120°, проведены лучи ОС и ОМ так, что угол АОС на 28° меньше угла ВОС, а OM — биссектриса угла ВОС. Найдите величину угла COM. ответ дайте в градусах.
Пусть у нас есть отрезок AB. Считаем, что он расположен в 1-й четверти координатной сетки и не параллелен осям координат (прочие положения отрезка рассматриваются аналогично). Координаты концов отрезка: A(x₁, y₁) и B(x₂, y₂). Допустим, что x₂>x₁. Пусть C - середина отрезка AB с координатами (x, y). Требуется выразить x и y через координаты точек A и B.
Определение координаты x. Из точек A, B и C отпустим перпендикуляры на отрезок OX, точки пересечения с осью OX обозначим A₁, B₁ и C₁.
AA₁⊥OX BB⊥OX CC⊥OX
Т.к. C - середина отрезка AB, то AC=BC. Т.к. AA₁||BB₁||CC₁, то по теореме Фалеса A₁C₁=B₁C₁. Значит, C₁ - середина отрезка A₁B₁.
Координаты точки A₁ равны (x₁;0). Координаты точки B₁ равны (x₂;0). Координаты точки C₁ равны (x;0).
Длина отрезка A₁C₁ равна x-x₁. Длина отрезка B₁C₁ равна x₂-x.
Эти длины равны, т.е. x-x₁=x₂-x ⇔ 2x=x₁+x₂ ⇔ x = (x₁+x₂) / 2.
Т.о., координата x середины отрезка есть полусумма координат x концов отрезка.
Определение координаты y. Выполняется аналогично, выполняя проекцию отрезка AB на координатную ось OY. y = (y₁+y₂) / 2
Т.о., координаты середины отрезка AB есть полусумма соответствующих координат концов отрезка.
Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами -
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: (*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: , где - координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)
Координаты концов отрезка: A(x₁, y₁) и B(x₂, y₂).
Допустим, что x₂>x₁.
Пусть C - середина отрезка AB с координатами (x, y).
Требуется выразить x и y через координаты точек A и B.
Определение координаты x.
Из точек A, B и C отпустим перпендикуляры на отрезок OX, точки пересечения с осью OX обозначим A₁, B₁ и C₁.
AA₁⊥OX
BB⊥OX
CC⊥OX
Т.к. C - середина отрезка AB, то AC=BC. Т.к. AA₁||BB₁||CC₁, то по теореме Фалеса A₁C₁=B₁C₁.
Значит, C₁ - середина отрезка A₁B₁.
Координаты точки A₁ равны (x₁;0).
Координаты точки B₁ равны (x₂;0).
Координаты точки C₁ равны (x;0).
Длина отрезка A₁C₁ равна x-x₁.
Длина отрезка B₁C₁ равна x₂-x.
Эти длины равны, т.е. x-x₁=x₂-x ⇔ 2x=x₁+x₂ ⇔ x = (x₁+x₂) / 2.
Т.о., координата x середины отрезка есть полусумма координат x концов отрезка.
Определение координаты y.
Выполняется аналогично, выполняя проекцию отрезка AB на координатную ось OY. y = (y₁+y₂) / 2
Т.о., координаты середины отрезка AB есть полусумма соответствующих координат концов отрезка.
C(x;y) = ((x₁+x₂) / 2; (y₁+y₂) / 2)
Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами -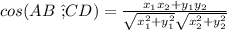
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: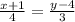
(*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: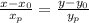
, где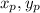 
- координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)