Многоугольник. Урок 2 Найди стороны четырехугольника ABCD, если его периметр равен 86 см, одна сторона меньше
второй на 7 см и на столько же больше третьей, а четвертая – на 5 см больше второй.
ответ:
Первая сторона АВ =
СМ;
Вторая сторона ВС=
СМ;
Третья сторона CD =
см;
Четвертая сторона DA =
СМ.​

К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в два раза меньше длины секущей. Найдите отношение длины касательной к длине радиуса.​

Объяснение:

По условию 2АМ=МС. Пусть радиус окружности r. Нужно найти .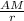

" Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB.  "

АМ²=МВ*МС , но длина отрезка МВ=МС-2r  ,

АМ²=( МС-2r)*2АМ |: АМ  ,    МС=2АМ  ,

АМ=(2АМ-2r)*2,

3АМ=4r      ⇒ .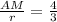

|60°|

Объяснение:

Можно решить задачу двумя

₍₁₎            У равнобедренной трапеции углы при основаниях равны.

                                                      ↓

                                            ∠С=∠D=120°

                                                      ↓

                        ∠A+∠B=360°-(120°+120°)=360°-240°=120°

            А т.к трапеция равнобедренная, то ∠А=∠В=120°:2=|60°|

₍₂₎          В равнобедренной трапеции основания параллельны.

           Углы D и А внутренние-односторонние при СD║АВ.                Внутренние-односторонние углы в сумме дают 180°

                                                  ↓    

                                  ∠А=180°-120°=|60°|