На биссектрисе сd равнобедренного треугольника авс взята точка м. через точку проведены прямые, параллельные сторонам ас и вс и пересекающие основания ав в точках н и к. докажите, что ан=кb.

Нет

Объяснение:

Сумма углов выпуклого многоугольника находится по формуле S = (n-2)*180°, где n - количество углов или сторон многоугольника.

Найдем по формуле сумму углов выпуклого семиугольника: S = (7 - 2)*180° = 5*180° = 900°.

Допустим, что наименьший угол 136°. Допустим, что все остальные углы равны, тогда они больше 136° на величину x°.

Тогда получим:  136° + 6*(136° + x°) = 900°

136° + 816° + 6x° = 900°

6x° = 900° - 952°

6x° = -52°

x =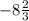 °, т.е. получаем противоречие, т.к. x - отрицательно, т.е остальные углы в таком случае меньше 136°, а значит 136° не наименьший угол.

ответ: нет

Формула для суммы внутренних углов выпуклого многоугольника 
N=180°*(n-2), где N - сумма углов, а  n- количество сторон многоугольника. Отсюда 
2700°=180°n-360°
3060°=180°n
n=3060:180=17

 Можно вторым решить, что, в принципе, одно и то же. 
Каждый внутренний угол выпуклого многоугольника образует с прилежащим к нему внешним углом угол 180°. 
А сумма ВСЕХ  внешних углов любого выпуклого многоугольника равна 360°
Следовательно, в данном случае сумма всех развернутых углов равна 
2700°+360°=3060°, а количество развернутых углов равно частному от деления суммы всех углов на 180°, т.е. на градусную меру развернутого угла. ответ, естественно, будет тем же - 17 сторон.