35°, 52°, 92°
Объяснение:
1) <BOC = 70°, => <BAC = 70° : 2 = 35° по свойству вписанного угла.
Т.к. <BOC = 70°, то дуга BC = 70° тоже по свойству центрального угла, тогда на дуга BAC = 360° - 70° = 290°.
2) По условию AB : AC = 4:7, => дуга AB + дуга AC = 4x + 7x = 290°
11x = 290°
x = 290 : 11 = 26 °
3) Дуга AB = 4x = 4*26 = 105 , => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105 : 2 = 52°
4) Дуга AC = 7x = 7*26 = 184 , => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184 : 2 = 92°
Докажите, что треугольник с вершинами A (-4; -1), B (2; -9), C (7; 1) равноБЕДРЕННЫЙ, и найдите длину биссектрисы к основаниЮ .
A (-4; -1), B (2; -9), C (7; 1)
АВ=√( (2+4)²+(-9+1)²)=√(36+64)=10
ВС=√( (7-2)²+(1+9)²)=√(25+100)=5√5
СА=√( (-4-7)²+(-1-1)²)=√(121+4)=√125=5√5⇒ ΔАВС-равнобедренный , т.к ВС=СА ⇒ АВ-основание.
Биссектриса в равнобедренном треугольнике является медианой. Пусть О-середина АВ , найдем ее координаты.
х(О)= ( х(А)+х(В) )/2 у(О)= ( у(А)+у(В) )/2
х(О)= ( -4+2 )/2 у(О)= ( -1-9 )/2
х(О)= -1 у(О)= -5
О( -1 ;-5) .
СО=√( -1-7)²+(-5-1)²=√(64+36)=√100=10
35°, 52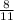 °, 92
°, 92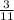 °
°
Объяснение:
1) <BOC = 70°, => <BAC = 70° : 2 = 35° по свойству вписанного угла.
Т.к. <BOC = 70°, то дуга BC = 70° тоже по свойству центрального угла, тогда на дуга BAC = 360° - 70° = 290°.
2) По условию AB : AC = 4:7, => дуга AB + дуга AC = 4x + 7x = 290°
11x = 290°
x = 290 : 11 = 26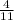 °
°
3) Дуга AB = 4x = 4*26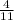 = 105
= 105 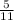 , => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105
, => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105 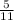 : 2 = 52
: 2 = 52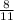 °
°
4) Дуга AC = 7x = 7*26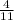 = 184
= 184 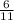 , => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184
, => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184 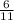 : 2 = 92
: 2 = 92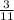 °
°
Докажите, что треугольник с вершинами A (-4; -1), B (2; -9), C (7; 1) равноБЕДРЕННЫЙ, и найдите длину биссектрисы к основаниЮ .
Объяснение:
A (-4; -1), B (2; -9), C (7; 1)
АВ=√( (2+4)²+(-9+1)²)=√(36+64)=10
ВС=√( (7-2)²+(1+9)²)=√(25+100)=5√5
СА=√( (-4-7)²+(-1-1)²)=√(121+4)=√125=5√5⇒ ΔАВС-равнобедренный , т.к ВС=СА ⇒ АВ-основание.
Биссектриса в равнобедренном треугольнике является медианой. Пусть О-середина АВ , найдем ее координаты.
х(О)= ( х(А)+х(В) )/2 у(О)= ( у(А)+у(В) )/2
х(О)= ( -4+2 )/2 у(О)= ( -1-9 )/2
х(О)= -1 у(О)= -5
О( -1 ;-5) .
СО=√( -1-7)²+(-5-1)²=√(64+36)=√100=10