1. опустим две высоты на большее основание трапеции. получим два прямоугольных треугольника, в которых известна гипотенуза (боковая сторона трапеции 6 см) и острый угол альфа. высота трапеции равна . часть большего основания . тогда, периметр равен . Площадь равна
2. медианы треугольнике пересекаються и точкой пересечения деляться в отношении 2:1, начиная от вершины треугольника. пусть медиана из вершины В треугольника АВС пересекает сторону АС в точке К. тогда по свойству медиан ОК=5 см. ВК = 15 см. рассмотрим треугольник ВСК. он прямоугольный (угол С = 90 градусов). Из теоремы пифагора
КС= 9 см. так как ВК медиана , то АК=КС=9 см. АС=18 см.
Сначала найдем периметр основания. 5+12+13=30см. Апофемой в данной пирамиде будет являться ребро, перепендикулярное плоскости основания, которое задано нам по условию.
Найдем площадь основания. Так как по условию в основании прямоугольный треугольник, мы можем найти его площадь по формуле Sосн=1/2bc, где b и c - катеты прямоугольного треугольника
Sосн=1/2*5*12=30 см^2
Площадь боковой поверхности пирамиды равна половине произведения периметра основания и апофемы: Sб=1/2P*l
Sб=1/2*30*9=135 см^2/
Площадь полной поверхности пирамиды равна сумме площади основания и площади боковой поверхности пирамиды
1. опустим две высоты на большее основание трапеции. получим два прямоугольных треугольника, в которых известна гипотенуза (боковая сторона трапеции 6 см) и острый угол альфа. высота трапеции равна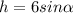 . часть большего основания
. часть большего основания 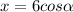 . тогда, периметр равен
. тогда, периметр равен 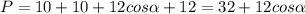 . Площадь равна
. Площадь равна 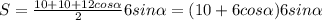
2. медианы треугольнике пересекаються и точкой пересечения деляться в отношении 2:1, начиная от вершины треугольника. пусть медиана из вершины В треугольника АВС пересекает сторону АС в точке К. тогда по свойству медиан ОК=5 см. ВК = 15 см. рассмотрим треугольник ВСК. он прямоугольный (угол С = 90 градусов). Из теоремы пифагора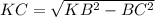
КС= 9 см. так как ВК медиана , то АК=КС=9 см. АС=18 см.
по теореме Пифагора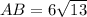 cv
cv
3. точка О где расположена?
Сначала найдем периметр основания. 5+12+13=30см. Апофемой в данной пирамиде будет являться ребро, перепендикулярное плоскости основания, которое задано нам по условию.
Найдем площадь основания. Так как по условию в основании прямоугольный треугольник, мы можем найти его площадь по формуле Sосн=1/2bc, где b и c - катеты прямоугольного треугольника
Sосн=1/2*5*12=30 см^2
Площадь боковой поверхности пирамиды равна половине произведения периметра основания и апофемы: Sб=1/2P*l
Sб=1/2*30*9=135 см^2/
Площадь полной поверхности пирамиды равна сумме площади основания и площади боковой поверхности пирамиды
Sп=Sосн+Sб
Sп=30+135=165 см^2
ответ: 165 см^2