На рисунке изображен график функции y=f(x) , на оси x отмечены точки a,b,c и d. Используя график, поставьте в соответствие каждой точке значение производной в ней.

Показать ответ

Ответ:

krikstoon1

15.06.2020 12:46

На рисунке треугольник ABC – равнобедренный (основание треугольника AC). Определите 2, если 1 = 56. 2. Угол , образованный при пересечении прямых n и k, равен 45, а угол , образованный при пересечении прямых m и k равен 135. Определите взаимное расположение прямых n и m. 1. прямые n и m перпендикулярны; 2. прямые n и m пересекаются, но не перпендикулярны; 3. прямые n и m параллельны; 4. такая ситуация невозможна. 3. В треугольнике АВС проведена медиана ВМ. Определите, какая из его сторон АВ или ВС больше, если ВМА = 80. 4. Две касающиеся окружности с центрами в точках O и O1 касаются сторон угла A (B и B1 – точки касания). Расстояние между точками A и O1 в два раза меньше, чем расстояние между центрами окружностей. Найдите радиус O1B1, если радиус OВ равен 24 см. 5. В треугольнике ABC углы, прилежащие к стороне AC, равны 30 и 45. Найдите отношение сторон AB и BC. 6. В прямоугольной трапеции АВСD (АВ  АD) боковая сторона CD в два раза больше стороны AB. Найдите градусную меру угла ВСD. 7. В четырехугольнике АВСD длины диагоналей АС и ВD равны соответственно 14 см и 18 см соответственно. Найдите периметр четырехугольника EFGH, вершинами которого являются середины сторон данного четырехугольника АВСD. 8. В ромб ABCD вписана окружность. Точка касания окружности G делит сторону ромба AB на отрезки AG и GB соответственно равные 2 см и 8 см. Найдите радиус вписанной окружности. 9. Определите, сколько решений имеет следующая задача. Решать задачу не надо. “В треугольнике ABC угол C равен 72, сторона AC равна 53 см, а сторона BC равна 37 см. Найдите сторону AB”. 10. В треугольнике ABC углы BAC и BCA равны 20 и 60 соответственно. Найдите угол между высотой BH и биссектрисой BD. 11. Две окружности с центрами в точках O и O1 и равными радиусами пересекаются в точках A и B. Определите вид четырехугольника AO1BO. 1. параллелограмм, отличный от прямоугольника и ромба; 2. прямоугольник; 3. ромб; 4. трапеция. 12. Определите, что больше: боковая сторона или основание равнобедренного треугольника, если один из его углов – тупой. 13. Отрезки AD и ВС пересекаются в точке О и распложены так, что прямые AB и CD параллельны. Известно, что AB = 18 см, CD = 9 см и CO = 6 см. Найдите длину отрезка BС. 14. Углы при основании AD трапеции ABCD равны 60 и 30, AD = 17 см, ВС = 7 см. Найдите СD. 15. Угол между высотами BL и BK параллелограмма АВСD, проведенными из вершины тупого угла, равен 52. Найдите величину угла ВАD. 16. Через точку G, лежащую на основании треугольника АВС, проведены отрезки GF 18. Дана окружность с центром О. По данным рисунка найдите градусную меру угла, обозначенного буквой . 19. В ромб ABCD с острым углом 30 вписана окружность радиуса 3 см. Найдите периметр ромба. 20. Определите, сколько решений имеет следующая задача. Решать задачу не надо. “В треугольнике ABC сторона AB равна 21 см, сторона BС равна 7 см, а угол C равен 33. Найдите сторону AС”. 21. Внутри равностороннего треугольника ABC отмечена точка D такая, что BAD = BCD = 15. Найдите угол ADC. 22. Прямые BD и AC пересекаются в точке О. В треугольниках BOC и AOD: BC = AD; BCO = OAD. Найдите ВО, если BD = 5 см. 23. Диагонали параллелограмма АВСD пересекаются в точке О. Определите, какая из его сторон ВС или CD меньше, если угол АОВ – острый. 24. В треугольник АВС вписан ромб ADEF так, что они имеют общий угол. Сторона ромба равна 5 см. Найдите сторону АВ треугольника АВС, если сторона AС равна 10 см. 25. Стороны треугольника равны 8 см, 15 см и 16 см. Определите вид этого треугольника. 1. треугольник – остроугольный; 2. треугольник – прямоугольный; 3. треугольник – тупоугольный; 4. такого треугольника не существует. 26. Найдите угол между биссектрисами углов A и B параллелограмма ABCD. 27. Диагонали трапеции ABCD являются биссектрисами ее углов при основании AD. Найдите периметр трапеции, если ее основания равны 12 см и 8 см. 28. Радиусы двух окружностей равны 4 см и 7 см, а расстояние между их центрами равно 12 с

0,0(0 оценок)

Ответ:

далина3

16.12.2022 18:35

Объяснение:

1) длины сторон АВ АС ВС

считаются по формуле

$\sqrt{(x2-x1)^{2}+(y2-y1)^{2}}$ .

Давайте рассмотрим на примере АВ.

А(1;5) В(2;-4)

АВ=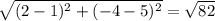 $\sqrt{(2-1)^{2}+(-4-5)^{2} } = \sqrt{82}$

2) уравнение прямой, проходящей через две точки с координатами А(х1,у1) и В(х2, у2) находится по формуле

$\frac{x-x1}{x2-x1} =\frac{y-y1}{y2-y1}$

Подставляем наши значения

$\frac{x-1}{2-1}=\frac{y-5}{-4-5}$

-9x+6=y

коэффициенты прямой k1=-9, b1=6

Проделав то же самое, но для прямой по координатам отрезка АС найдем

у=4х+1 , k2=4, b1=1

3) зная два уравнения прямых мы сможем найти угол, которые они образуют при пересечении

$tg\alpha =\frac{k2-k1}{1+k2k1}=\frac{4-(-9)}{1+(-9)•4}=\frac{13}{35}$

tgα=13/35 ⇒ arctg13/35 ≈ 20°

3) УРАВНЕНИЕ ВЫСОТЫ, проведенной через вершину С

Прямая, к которой проведен перпендикуляр описывается уравнением -9x+6=y

k1=-9

Для двух ⊥-ых прямых должно выполняться условие k1*k2=1

т/е подбираем коэффициент k2 для уравнения высоты, поскольку высота треугольника это перпендикуляр, опущенный из вершины. Несложно догадаться, что k2 будет -1/9

Прямая, проходящая через точку N0 (х0, у0)( в нашем случае это С (0, 1) описывается уравнением:

y-y0=k(x-x0) .