1 — неправильно. Бывают ситуации, что у них углы равны между собой, но длины их сторон разные, но они при этом пропорциональны. Такие треугольники называются подобными. 2 — неверно, такой отрезок называется радиусом, а диаметр — хорда, проходящая через центр окружности. 3 — верно, в равнобедренном треугольнике биссектриса, проведённая к основанию, является и медианой, и высотой этого треугольника. 4 — верно, многие об этом знают, если вы ,конечно, читали определение этой фигуры. 5 — верно, это все-таки смежные углы. 6 — неверно, в равнобедренном треугольнике он обязан лежать на противолежащей основанию вершине. 7 — нет, сумма смежных углов равна 180° и по определению острый угл — угл, который меньше угла в 90°. Значит угл смежный острому должен быть тупым. 8 — нет. Прямые могут иметь одну общую точку, но есть ещё прямые, которые совпадают между собой и прямые, не имеющие ни одной общей точки(параллельные прямые).
2 — неверно, такой отрезок называется радиусом, а диаметр — хорда, проходящая через центр окружности.
3 — верно, в равнобедренном треугольнике биссектриса, проведённая к основанию, является и медианой, и высотой этого треугольника.
4 — верно, многие об этом знают, если вы ,конечно, читали определение этой фигуры.
5 — верно, это все-таки смежные углы.
6 — неверно, в равнобедренном треугольнике он обязан лежать на противолежащей основанию вершине.
7 — нет, сумма смежных углов равна 180° и по определению острый угл — угл, который меньше угла в 90°. Значит угл смежный острому должен быть тупым.
8 — нет. Прямые могут иметь одну общую точку, но есть ещё прямые, которые совпадают между собой и прямые, не имеющие ни одной общей точки(параллельные прямые).
Найти периметр трапеции по готовому чертежу
Объяснение:
∠BCО = ∠ОЕА= 30° как накрест лежащие , при секущей СЕ.
По т. о внешнем угле треугольника в ΔЕАО , ∠ЕОА=60°-30°=30°. Откуда ∠AOE = ∠BOC = 30° ⇒ ∠ВОС=30°.
Значит ΔЕАО=ΔСВО по стороне и 2-м прилежащим углам:
ОА=ОВ по условию,
∠AOE = ∠BOC = 30° ,
∠ЕАО=∠СВО как накрест лежащие ,АВ-секущая.
В равных треугольниках соответственные элементы равны ⇒ЕА=ВС.
Пусть ЕА=ВС=а. Т.к. ΔЕАО , ΔСВО-равнобедренные , то ЕА=ОА=ВС=ОВ=а . Тогда сторона трапеции АВ=2а ⇒ СD=2а (*),
т.к АВСD-равнобедренная трапеция( ∠D=180°-120°=60°)
Из Δ ECD -прямоугольный , ЕD=ЕА+АD=а+15 найдем C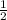D =
ED =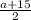
(**).
Приравняем полученные выражения (*) и (**) , получим
2а =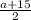
, 4а=а+15 , а=5 ⇒ ВС=5, АВ=СD=10
P(ABCD) = 5 + 15 +2* 10 =40 .