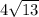На рисунке угол dbc = углу cad, угол bo = углу ao. докажите, что угол c = углу d. найдите ac, если bd = 12 сма если у кого есть ответы на все билеты то скиньте )
К этому не уточненному условию можно подобрать разные конфигурации "параллелограмм-высота" – если выберем конфигурацию с большим тупым углом в вершине Mтак, что опустим высоту в точку E на сторону NP, то следует, что треугольник MNE - прямоугольный, поэтому MNE + NME = 90 градусов. А угол MNP - это = углу MNE. Вот и получаем, что 6MNE = 90 => MNE = 15 градусов, т.е. MNP = 15. Параллелограмм с углами KMNи NPK= 165 градусов. P.S. Вершину M можно расположить в остром угле, тогда высота параллелограмма будет с внешней стороны фигуры.
Но Я буду думать и над предыдущим. Я уверен, что и там есть решение.
от точки А проведем перепендикуляр ко второй параллельной прямой, эту точку пересечения обозначим А1 - она является высотой в треугольнике АВС и равна 4 см.
точку С соединим с центром окружности (точкой О). полученный отрезок ОС-радиус=6,5см.
Если АО-радиус и равен 6,5 см, а АА1=4 см, то найдём ОА1=АО-АА1=6,5см-4см=2,5см.
образовался треугольник ОСА1. в неём нам известны гепатенуза (ОС=6,5см) и катет (ОА1=2,5 см). по теореме пифагора найдём второй катет
ВС=
В треугольнике теперь нам известны высота (АА1=4см) и катет (ВС=.
По формуле. которая дана в начале. находим площадь.
Я уже давал другое решение, вот оно:
К этому не уточненному условию можно подобрать разные конфигурации "параллелограмм-высота" – если выберем конфигурацию с большим тупым углом в вершине Mтак, что опустим высоту в точку E на сторону NP, то следует, что треугольник MNE - прямоугольный, поэтому MNE + NME = 90 градусов. А угол MNP - это = углу MNE.
Вот и получаем, что 6MNE = 90 => MNE = 15 градусов, т.е. MNP = 15. Параллелограмм с углами KMNи NPK= 165 градусов. P.S. Вершину M можно расположить в остром угле, тогда высота параллелограмма будет с внешней стороны фигуры.
Но Я буду думать и над предыдущим. Я уверен, что и там есть решение.
S=1/2 а*h
от точки А проведем перепендикуляр ко второй параллельной прямой, эту точку пересечения обозначим А1 - она является высотой в треугольнике АВС и равна 4 см.
точку С соединим с центром окружности (точкой О). полученный отрезок ОС-радиус=6,5см.
Если АО-радиус и равен 6,5 см, а АА1=4 см, то найдём ОА1=АО-АА1=6,5см-4см=2,5см.
образовался треугольник ОСА1. в неём нам известны гепатенуза (ОС=6,5см) и катет (ОА1=2,5 см). по теореме пифагора найдём второй катет
ВС=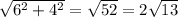
В треугольнике теперь нам известны высота (АА1=4см) и катет (ВС=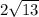 .
.
По формуле. которая дана в начале. находим площадь.
S=1/2*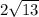 *4=
*4=