Отрезок DC - перпендикуляр к плоскости треугольника АВС. Найдите площадь треугольника АDB, если <АСВ = 90 °, АС = 5см, АВ = 13см, а угол между плоскостями АВС и АВD равен 45°.
Объяснение:
1) Т.к. угол между плоскостями АВС и АВD равен 45° , то построим линейный угол данного двугранного. Пусть DH ⊥AB, тогда по т. о трех перпендикулярах СН⊥АВ. Значит ∠СНD линейный угол данного двугранного ∠СНD =45°.
2)S(ABD)=1/2*АВ*DH .Найдем DH
3)ΔАВС-прямоугольный , по т. Пифагора СВ=√(13²-5²)=12 (см).
По метрическим соотношениям о среднем пропорциональном в прямоугольном треугольнике :
СВ²=АВ*НВ , 12²=13*НВ , НВ = (см) .
Тогда АН=АВ-НВ =13- = (см).
СН = , CH= (см).
4)ΔCHD-прямоугольный , ∠CHD=45° . sin45°= , = ,DH= см.
Пусть общая высота конуса и пирамиды равна Н.
Обозначим объемы конуса и пирамиды через V1 и V2 соответственно ,
а их боковые поверхности – через S1 и S2
тогда V1=1/3pi*R^3H , S1=pi*RL ,
где L-образующая конуса.
Найдем V2 и S2.
Так как периметр основания пирамиды равен 2р ,
а основание конуса – вписанная в основание пирамиды окружность,
то площадь основания пирамиды равна pR,
откуда V2=1/3pRH, S2=pL (высота любой грани равна L).
Тогда
V1 : V2 =1/3piR^2H : 1/3pRH = pi*R/p
S1 : S2 =pi*RL : pL = pi*R/p
ответ V1 : V2 = S1 : S2 = pi*R/p
Отрезок DC - перпендикуляр к плоскости треугольника АВС. Найдите площадь треугольника АDB, если <АСВ = 90 °, АС = 5см, АВ = 13см, а угол между плоскостями АВС и АВD равен 45°.
Объяснение:
1) Т.к. угол между плоскостями АВС и АВD равен 45° , то построим линейный угол данного двугранного. Пусть DH ⊥AB, тогда по т. о трех перпендикулярах СН⊥АВ. Значит ∠СНD линейный угол данного двугранного ∠СНD =45°.
2)S(ABD)=1/2*АВ*DH .Найдем DH
3)ΔАВС-прямоугольный , по т. Пифагора СВ=√(13²-5²)=12 (см).
По метрическим соотношениям о среднем пропорциональном в прямоугольном треугольнике :
СВ²=АВ*НВ , 12²=13*НВ , НВ =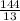 (см) .
(см) .
Тогда АН=АВ-НВ =13-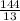 =
=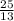 (см).
(см).
СН =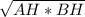 , CH=
, CH=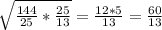 (см).
(см).
4)ΔCHD-прямоугольный , ∠CHD=45° . sin45°=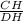 ,
, 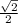 =
= 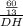 ,DH=
,DH=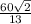 см.
см.
5) S(ABD)=1/2*13*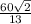 =30√2 (см²).
=30√2 (см²).