На рисунку зображено розгортку конуса, у якому l=10 см, r=6 см. установіть відповідність між величинами(1-3) та їхніми значеннями (а-г). фото внизу. будь ласка, іть по старій дружбі)
Из точки С проведены две наклонные к точкам А и В на прямой. Перпендикуляр опущенный из точки С на прямую АВ делит отпезок АВ на два АО = 9 см. и ВО = 16см. Наклонная СВ на 5 см. больше наклонной СА.
У нас два прямоугольных треугольника АОС и ВСО. Углы АОС и ВОС - прямые. АО и ВО - гипотенузы. Расстояние от точки С - катет СО - общий для обоих треугольников.
ΔАОД - равнобедренный (ОА=ОД=R), т.к. АВ=ВД (В - середина АД), то ОВ - медиана. Медиана в равнобедренном Δ является также высотой ⇒ОМ⊥АД.
Четырёхугольник АОДМ: Диагонали перпендикулярны, а если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны:
Відповідь:
Расстояние от точки до прямой 12 см.
Пояснення:
Из точки С проведены две наклонные к точкам А и В на прямой. Перпендикуляр опущенный из точки С на прямую АВ делит отпезок АВ на два АО = 9 см. и ВО = 16см. Наклонная СВ на 5 см. больше наклонной СА.
У нас два прямоугольных треугольника АОС и ВСО. Углы АОС и ВОС - прямые. АО и ВО - гипотенузы. Расстояние от точки С - катет СО - общий для обоих треугольников.
Пусть АО = х, тогда ВО = х + 5.
По теореме пифагора:
СО^2 = х^2 - 9^2
СО^2 = (х + 5)^2 - 16^2
х^2 - 81 = х^2 + 10х + 25 - 256
х в квадрате сокращается.
10х = 256 - 81 - 25 = 150
х = 15 см.
Подставим х в первое уравнение.
СО^2 = 15^2 - 9^2 = 225 - 81 = 144
СО = 12 см.
АД =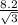
Периметр ΔАОД = 8,2√3
Объяснение:
ΔАОД - равнобедренный (ОА=ОД=R), т.к. АВ=ВД (В - середина АД), то ОВ - медиана. Медиана в равнобедренном Δ является также высотой ⇒ОМ⊥АД.
Четырёхугольник АОДМ: Диагонали перпендикулярны, а если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны:
АО²+ДМ²=ОД²+АМ²
АО=ОД=R ⇒ R²+ДМ²=R²+АМ²
⇒ДМ=АМ ⇒ Четырёхугольник АОДМ - ромб,
ОА=ОД=ДМ=АМ=R
Рассмотрим ΔАОВ(∠В=90°). ОВ=1/2ОМ (св-во диагоналей ромба)
ОМ=1/2 ТМ ⇒ ОВ=1/4 ТМ = 1/4* 16,4 = 4,1 см
∠О=30°.
ОА=R=ОВ/cos 30° =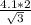 =
= 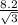
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
АВ=1/2 ОА = 1/2 *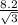 =
= 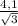 , т.к. В - середина АД, то
, т.к. В - середина АД, то
АД = 2*АВ=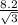
Периметр ΔАОД = 2*ОА+АД= 2*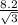 +
+ 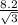 = 8,2√3
= 8,2√3