На сторонах AB, BC, CD, DA квадрата ABCD выбраны точки P, Q, R, S соответственно. Выберите все верные утверждения.

Если отрезки PR и QS равны, то они перпендикулярны

Если отрезки PR и QS перпендикулярны, то они равны

Если отрезки PR и QS равны и перпендикулярны, то PQRS является квадратом

Если вокруг четырёхугольника PQRS описан прямоугольник, то этот прямоугольник является квадратом

Если отрезки PR и QS перпендикулярны и вокруг четырёхугольника PQRS описан прямоугольник, то этот прямоугольник является квадратом

Если отрезки PR и QS равны и вокруг четырёхугольника PQRS описан прямоугольник, то этот прямоугольник является квадратом

Я знаю первое))

Дано:тр-к АВС,АВ=ВС=17,ВД-высота_cosA=8/17 Найти:ВД Pешение: 1)cosA=AD/AB=>8/17=AD/17=>AD=8. 2)BD²=AB²-AD²;BD²=17²-8²=(17-8)(17+8)=9*25=>BD=3*5=15.

А второе только без дано((

Пусть высота проведенная к большей  стороне(АД) - ВН. Площадь параллелограмма равна произведению основания на высоту проведенную к этому основнию, значит S=BH*AD=14*4=56(см)^2-площадь параллелограмма. 

Обозначим вторую высоту проведенную к стороне СД, как АК, тогда по формуле площади парллелограмма имеем:

S=AK*CD, отсюда АК=S/CD=56/8=7(см).

ответ: 56см^2, 7см.

Дано: ABCD - трапеция

           AM = MB

           CP = PD

          BC // MP // AD

          MP = 3

          BC = 5

Найти: AD

MP - средняя линия трапеции ABCD ( по определению средней линии:  отрезок, соединяющий середины боковых сторон трапеции, называется средней линией этой трапеции )

Длинна средней линии находится по формуле ⇒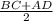  

ответ: AD = 1

P.s - мне кажется, правильнее было бы верхнее основанее  назвать AD, а нижнее BC ( так как верхнее основанее не может быть больше средней линии, а нижнее не может быть меньше)

⇒  фото чтобы вы поняли, что я имею ввиду