На сторонах ОА и OB угла АОВ отмечены точки Си D соответственно так, что углы BCO и ADO равны, ОС = OD, OA = 15 см, ОС = 8 см, ВС = 9 см. Найдите периметр треугольника DBM (в см), где м – точка пересечения отрезков BC и AD. =
Дано: АВСД - равнобед. трапеция, АД=16,большее основание, АВ=ВС=10 боковые стороны, один из углов = 60 Найти: ВС Решение: Проведем высоту к основанию АД из углов АВС (высота ВН) и угла ВСД (высота СК). Рассмотрим треугольники АВН и СКД, они прямоугольные. Найдем неизвестные углы (АВН и КСД) : 180 - (АНВ+ВАН) = АВН или 180 - (ДКС+СДК) = КСД 180 - (90+60)=30 По свойству прямоугольного треугольника => против угла 30 градусов лежит катет, равный половине гипотенузы. АВ=СД=10 Отсюда следует, что АН = СД =5 16 - (5+5) =6 ответ: 6
Итак, у нас есть равнобедренный треугольник со сторонами 5, 5, 8. И нужно найти его площадь. Например, по формуле:
S = (1/2)ah, где а - основание, а h - высота.
Но высоту мы не знаем. Попробуем ее найти. В предлагающемся ниже рисунке видно, что можно разделить этот треугольник на два прямоугольных одинаковых треугольника, у каждого из которых основание по 8/2 = 4, а гипотенуза - 5. Поэтому общая высота, по теореме Пифагора (сумма квадратов равна квадрату гипотенузы), равна . Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
S = (1/2)*3*8 = 12.
Следовательно, площадь данного треугольника равна 12 (номер ответа - 3).
Найти: ВС
Решение: Проведем высоту к основанию АД из углов АВС (высота ВН) и угла ВСД (высота СК). Рассмотрим треугольники АВН и СКД, они прямоугольные. Найдем неизвестные углы (АВН и КСД) :
180 - (АНВ+ВАН) = АВН или 180 - (ДКС+СДК) = КСД
180 - (90+60)=30
По свойству прямоугольного треугольника => против угла 30 градусов лежит катет, равный половине гипотенузы. АВ=СД=10
Отсюда следует, что АН = СД =5
16 - (5+5) =6
ответ: 6
ответ: 3) 12.
Итак, у нас есть равнобедренный треугольник со сторонами 5, 5, 8. И нужно найти его площадь. Например, по формуле:
S = (1/2)ah, где а - основание, а h - высота.
Но высоту мы не знаем. Попробуем ее найти. В предлагающемся ниже рисунке видно, что можно разделить этот треугольник на два прямоугольных одинаковых треугольника, у каждого из которых основание по 8/2 = 4, а гипотенуза - 5. Поэтому общая высота, по теореме Пифагора (сумма квадратов равна квадрату гипотенузы), равна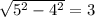 . Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
. Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
S = (1/2)*3*8 = 12.
Следовательно, площадь данного треугольника равна 12 (номер ответа - 3).