На сторонах угла ∡ ABC точки A и C находятся на равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥ BD, CD⊥ BE. 1. Докажи равенство треугольников ΔAFD и ΔCFE.
2. Определи величину угла, под которым перпендикуляр CD пересекает BA, если AE пересекает BC под углом 73°.

1. Назови треугольники, равенство которых позволит доказать равенство ΔAFD и ΔCFE:
ΔBA
= Δ
.

По какому признаку доказывается это равенство?
По второму
По первому
По третьему

Отметь элементы, равенство которых в этих треугольниках позволяет применять выбранный признак:

углы стороны
ABE
BEA
CBD
EAB
DCB
BDC

CD
BC
BA
AE
DB
EB

По какому признаку доказывается равенство ΔAFD и ΔCFE?
По третьему
По второму
По первому

Отметь элементы, равенство которых в треугольниках ΔAFD и ΔCFE позволяет применять выбранный признак:

углы стороны
CEF
ADF
DFA
EFC
FAD
FCE

FC
CE
EF
AD
DF
FA

2. Величина угла, под которым перпендикуляр CD пересекает

60 градусов каждый угол треугольника АВД

Объяснение:

1)Треугольник АВД равнобедренный, т.к. стороны АД=АВ. Значит высота, проведенная из вершины А к основанию ВД, является еще и медианой и биссектрисой. В этом случае ВС=СД.

2)Рассмотрим один из получившихся прямоугольных треугольников, например, АВС. В треугольнике мы видим, что ГИПОТЕНУЗА В ДВА РАЗА БОЛЬШЕ КАТЕТА, А ЭТО ЗНАЧИТ,ЧТО УГОЛ,НАПРОТИВ ЭТОГО КАТЕТА РАВЕН 30 ГРАДУСОВ.(ВАС)

3)Так как треугольник прямоугольный найдём его третий угол АВС 180-30-90=60 ГРАДУСОВ.

4)Далее, вспоминаем, что АВД- РАВНОБЕДРЕННЫЙ треугольник и вспоминаем, что углы при его основании равны, значит, АВД=АДВ=60 ГРАДУСОВ.

5)И теперь находим угол ДАВ 180-60-60=60 ГРАДУСОВ. Треугольник равносторонний, все углы по 60 градусов.

ИЛИ  

2)Т.к. ВС=СД, ТО ВД=ВС=СД=7

3)Так как все стороны 7, то треугольник равносторонний, и все его углы равны. (180/3=60 градусов)

∠ 1 = ?°, на 55° больше, чем ∠ 2.

∠ 2 = ?°

Оба угла являются смежными.

Пусть x° равен смежный ∠ 2, тогда ∠ 1 равен (55+x)˚. Зная, что свойство смежных углов всегда содержит сумму 180°, составим уравнение с переменными и решим задачу алгебраическим

Составление математической модели:

Работа с математической моделью:

Поскольку уравнение имеет переменные, раскроем скобки и найдём значение переменных:

Теперь, зная что число с переменной и число без переменной в данном случае вычислить невозможно, перенесем число без переменной в правую часть уравнения (число становится отрицательным):

Затем вычислим полученный пример, находящийся в правой части уравнения:

Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:

ответ математической модели:

Исходя из значения данного примера, получим корень уравнения:

˚ - ∠ 2.

Теперь остаётся только узнать величину ∠ 1:

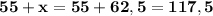˚ - ∠ 1.