На точку A действуют две силы AB−→− и AC−→− одинаковой величины.
Угол между ними ∡A=50°.
Определи величину приложенных сил, если в результате на точку A действует сила величиной 73 N (округли результат до целых).
ответ: величина сил AB−→− и AC−→− равна
N.
a)
В единственной картинке.
b)
Так как хорда SF — равна радиусу, то треугольник OFS, образованный двумя радиусами и хордой SF — правильный.
То есть: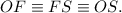
HL — диаметр, перпендикулярный хорде SF, то есть: OM ⊥ SF.
То есть отрезок OM — высота, проведённая к основанию, а в правильном треугольнике, высота, биссектриса и медиана, проведённые к основанию — одно и то же.
То есть OM — медиана, что и означает, что:
Вывод: FS = 16.4см.
c)
Так как OM — высота треугольника OFS, проведённая к основанию, то треугольники OFM & OSM — прямоугольные, так как каждый из них имеет прямой угол (<OMF; <OMS).
OF — гипотенуза, FM — катет, чтобы найти второй катет, то есть OM, используем теорему Пифагора:
Диаметр равен половине отрезка OM, то есть: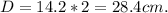
Вывод: Диаметр HL равен 28.4см.
d)
Как я говорила ранее — треугольник OSF — правильный, то есть все стороны равны, то есть:
Вывод: Периметр треугольника OSF равен 49.2см.
Відповідь:
80 см.
Пояснення:
Хорда та два радіуси проведені із центра кола до її кінців утворюють рівнобедренний трикутник. Проведемо в цьому трикутнику висоту. Вона ділить наш трикутник на дві однакові частини - кожна з них - це прямокутний трикутник з гіпотенузою 100 см. та катетом 120 / 2 = 60 см. Розділимо сторони цього трикутника на 20. Утворюється прямокутний трикутник подібний нашому, але зі сторонами 5 ( гіпотенуза ) та 3 ( катет ). Цей трикутник носить назву єгипетьського з співвідношенням сторін 5 ÷ 4 ÷ 3. Невідомий нам катет дорівнює 4. Повернемось до нашого трикутника, помножемо 4 на 20 та отримаємо відповідь на питання задачі.
4 × 20 = 80 см.