б) Аналогично с (a). Угол на нижнем треугольнике: 180-90-50=40
Треугольники равны по стороне и двум углам.
в) В прямоугольном треугольнике, сторона, противолежащая углу в 30 равна половине гипотенузы. Следовательно:
на верхнем треугольнике гипотенуза равна 2*4 = 8
На нижнем треугольнике угол равен 30
Дальше можно найти третью сторону по теореме Пифагора и применить признак по трем сторонам, либо найти третий угол и применить признак по двум сторонам и углу между ними.
Нижняя сторона равна
Верхний угол равен 180-90-30=60
Если что-то непонятно - пишите, я уточню!
============
Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Т.к. трапеция равнобоковая, то две высоты, проведённые из меньшего основания к большему, будут равны, параллельны, будут отсекать на большем основании три отрезка, один из которых (центральный) равен меньшему основанию, а два других равны (исходя из равенства получившихся треугольников, которые равны по катета и гипотенузе). Находим далее эти равные отрезки. Вычитаем из длины большего основания меньшее и делим на два. Получаем 4 см. Т.к. диагонали перпендикулярны сторонам, то находим высоту треугольника как среднее геометрическое. Среднее геометрическое равно корню из произведения проекций катетов, т.е. высота равна √(4*(12+4)) = √(4*16) = √64 = 8 см. Значит, высота равна 8 см.
a) Угол на нижнем треугольнике: 180-90-60=30
Треугольники равны по стороне и двум углам
б) Аналогично с (a). Угол на нижнем треугольнике: 180-90-50=40
Треугольники равны по стороне и двум углам.
в) В прямоугольном треугольнике, сторона, противолежащая углу в 30 равна половине гипотенузы. Следовательно:
на верхнем треугольнике гипотенуза равна 2*4 = 8
На нижнем треугольнике угол равен 30
Дальше можно найти третью сторону по теореме Пифагора и применить признак по трем сторонам, либо найти третий угол и применить признак по двум сторонам и углу между ними.
Нижняя сторона равна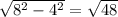
Верхний угол равен 180-90-30=60
Если что-то непонятно - пишите, я уточню!
============
Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!