1) Проведём две высоты к плоскости ABCD из вершин и И отметим их как и соответственно.
2)Рассмотрим полученный треугольник ; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна , то можно и найти
(Против угла в 30 градусов лежит катет равный половине гипотенузы).
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника:
5)Следует детально рассмотреть треугольник В нем известны две стороны, и он прямоугольный, а значит можно найти по теореме Пифагора. .
6)Отсюда можно найти .
. Знаю эту величину можем найти искомую АB.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат. ; Но также стоит заметить, что , но второй намного легче, чем мучиться с преобразованием корневых выражений.
Дано:
Найти: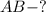
1) Проведём две высоты к плоскости ABCD из вершин
и 
И 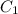отметим их как 
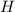и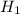 
соответственно.
2)Рассмотрим полученный треугольник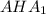
; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна 
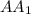, то можно и найти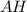 
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем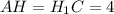
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника: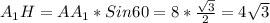
5)Следует детально рассмотреть треугольник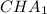
В нем известны две стороны, и он прямоугольный, а значит можно найти 
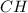по теореме Пифагора. 
.
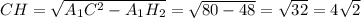6)Отсюда можно найти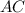
.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат.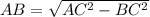
; Но также стоит заметить, что 
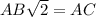, но второй намного легче, чем мучиться с преобразованием корневых выражений.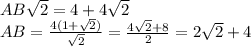 
ответ: AB= двум корней из двух плюс 4
Объяснение:
1) Т.к. АВ=ВС, то треугольник АВС-р/б, следовательно, ВD - медиана, биссектриса, высота.
Т.к. ВD - биссектриса, то в треугольнике АВD угол АВD= 120°:2=60°
Т.к. ВD - высота, то в треугольнике АВD угол АDВ = 90°
Сумма углов треугольника равна 180°, следовательно, угол ВАD = 180°-(60°+90°)=180°-150°=30°.
2) Мы узнали, что угол ВАD=30°, найдём длину ВD.
Треугольник АВD - прямоугольный.
В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.
Угол ВАD = 30°, угол ВАD лежит напротив ВD, следовательно ВD = 0,5АВ=0,5×18=9 (см).
ответ: 1) 60°, 90°, 30°.
2) 9 см.
Вот чертёж, дано, надеюсь, напишешь.