2) Площадь по формуле Герона. S = √(p(p-a)(p-b)(p-c). Подставив данные, получаем: Треугольник АВС a(ВС) b(АС) c(АВ) p 2p S 6,4807 10,7703 6,4807 11,8659 23,7318 19,4165 cos A = 0,830949 cos B = -0,3809523 cos С = 0,830949 Аrad = 0,5899851 Brad = 1,961622457 Сrad = 0,5899851 Аgr = 33,8036561 Bgr = 112,3926878 Сgr = 33,803656/ Площадь равна 19,4165 кв.ед.
Координаты т. А Координаты т. В Координаты т. С
ax ay az bx by bz cx cy cz
3 -1 2 -1 4 1 -5 3 -4.
1) Расстояние между точками.
d = v ((х2 - х1 )² + (у2 - у1 )² + (z2 – z1 )²)
АВ ВС АС Периметр Полупериметр
42 42 116 квадрат
6,4807 6,4807 10,7703 23,7318 11,8659
Вектор АВ -4 5 -1 |AB| = √(16+25+1) = √42 = 6,4807
Вектор ВС -4 -1 -5 |BC| = √(16+1+25) = √42 = 6,4807
Вектор АС -8 4 -6 |AC| = √(64+16+36) = √116 = 10,7703.
Р = 23,7318.
2) Площадь по формуле Герона.
S = √(p(p-a)(p-b)(p-c).
Подставив данные, получаем:
Треугольник АВС
a(ВС) b(АС) c(АВ) p 2p S
6,4807 10,7703 6,4807 11,8659 23,7318 19,4165
cos A = 0,830949 cos B = -0,3809523 cos С = 0,830949
Аrad = 0,5899851 Brad = 1,961622457 Сrad = 0,5899851
Аgr = 33,8036561 Bgr = 112,3926878 Сgr = 33,803656/
Площадь равна 19,4165 кв.ед.
1.
P(4;3), T(-2;5).
Используем уравнение прямой, проходящей через две точки.
Если даны две точки A(x₁; y₁) и B(x₂; y₂), тогда уравнение прямой, проходящей через эти две точки будет
То есть у нас даны две точки P(4;3) и T(-2;5), уравнение прямой, проходящей через них будет
-(x-4) = 3·(y-3),
4 - x = 3y - 9,
3y + x - 9 - 4 = 0,
x + 3y - 13 = 0.
Можно сделать проверку: подставим координаты каждой точки в уравнение и проверим выполнение равенства.
P(4;3):
4 + 3·3 - 13 = 4 + 9 - 13 = 0. Верно.
T(-2;5):
(-2) + 3·5 - 13 = -2 + 15 - 13 = 0. Верно.
ответ. x + 3y - 13 = 0.
2.
x + 3y - 13 = 0,
Уравнение оси Ox (оси абсцисс): y = 0. Подставим это в уравнение прямой и получим x + 3·0 - 13 = 0, ⇔ x = 13.
Итак, пересечение прямой с осью Ox дает точку (13;0).
Уравнение оси Oy (оси ординат): x = 0. Подставим это в уравнение прямой и получим 0 + 3y - 13 = 0, ⇔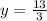 .
.
Итак, пересечение прямой с осью Oy в точке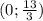 .
.
3.
Дана прямая x - y + 2 = 0 и окружность (x-2)² + (y-1)² = 9.
Чтобы найти координаты точек пересечения решим систему двух уравнений на два неизвестных.
Из уравнения прямой находим y = x+2, подставим это в уравнение окружности: (x-2)² + ( x+2 - 1)² = 9,
(x-2)² + (x+1)² = 9,
x² - 4x + 4 + x² + 2x + 1 = 9,
2x² - 2x + 5 - 9 = 0,
2x² - 2x - 4 = 0,
x² - x - 2 = 0,
D = (-1)² - 4·1·(-2) = 1 + 8 = 9 = 3²,
Итак, координаты первой точки (-1; 1).
Итак, координаты второй точки (2; 4).
ответ. (-1; 1), (2; 4).