Напишите уравнение окружности с диаметром МК, если М(8;-5) и К(-4;1)

Показать ответ

Ответ:

Снежана1995

19.06.2020 19:32

ответ:1) так как треугольник АBC равно едренный => BD- медиана, высота, биссектриса=> угол ADB=90 градусов;

Так как BD- биссектриса=>угол ABD= углу DBС= угол ABC/2=78/2=39 градусов

ответ:90;39

2)так как D-середина AB=>BD=AD; так как Е-середина ВС=>СЕ=ВЕ; так как AD=EC=>BD=AD=CE=BE и AB=BC;

Треуголники АВЕ и СDB равны по двум сторонам и углу сежду ними(DB=BE; AB=BC; угол В- общий) Ч. Т. Д.

3)треугольники ОАВ и СОD равны по двум углам и ребру между ними ( OA=OC- по условию; угол А=углу С- по условию; угол О- общий) Ч. Т. Д.;

Так как треуголники равны=> у них все ребра тоже равны=> АВ=DC=15см

ответ: 15см

Объяснение:

0,0(0 оценок)

Ответ:

Aigerim800

17.12.2021 23:46

Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.

Перший б

Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:

$a^{2} = a_{c}c \Rightarrow a = \sqrt{a_{c}(a_{c}+ b_{c})} = \sqrt{6 \cdot (6 + 24)} = \sqrt{180} = 6\sqrt{5}$ см

$b^{2} = b_{c}c \Rightarrow a = \sqrt{b_{c}(a_{c}+ b_{c})} = \sqrt{24 \cdot (6 + 24)} = \sqrt{720} = 12\sqrt{5}$ см

Площа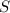 прямокутного трикутника знаходится як півдобуток його катетів:

$S = \dfrac{a \cdot b}{2} = \dfrac{6\sqrt{5} \cdot 12\sqrt{5}}{2} = 180$ см²

Другий б

Висота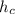 $h_{c}$ прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:

$h^{2}_{c} = a_{c}b_{c} \Rightarrow h_{c} = \sqrt{a_{c}b_{c}} = \sqrt{6 \cdot 24} = \sqrt{144} = 12$ см

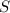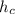Площа будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти $h_{c}$ , що до неї проведена:

$S = \dfrac{1}{2} \cdot c \cdot h_{c} = \dfrac{1}{2} \cdot (6 + 24) \cdot 12 = 30 \cdot 6 = 180$ см²