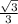Нарисуйте четырёхугольник, который можно разрезать пополам (точнее, на два одинаковых четырёхугольника) отрезком, который делит одну из сторон разрезаемого четырёхугольника пополам, а другую на две отрезка, один из которых в два раза длиннее другого.
Нехай Сейчас ΔАВС - рівнобедреній (АВ = ВС), висоти проведені iз кутів A i С.
АК i CD - висоти, т. Про - точка їx перетин, ∟АОС = 100 °.
Знайдемо куті ΔАВС.
∟DOA = ∟AOC = 180 ° (як суміжні).
∟DOA = 180 ° - 100 ° = 80 °. ∟DOA = ∟КОС = 80 ° (як вертикальні).
Розглянемо ΔАВК. ∟AKB = 90 °, ∟DAO = ∟KCO = 180 ° - (90 ° + 80 °) = 10 °,
∟ВАК = 10 °, тоді ∟АВК = 90 ° - 10 ° = 80 °.
Розглянемо ΔАВС - рівнобедреній, ∟В = 80 °.
∟ВАС = ∟ВСА = (180 ° - 80 °): 2 = 50 °.
Biдповідь: ∟В = 80 °, ∟ВАС = ∟ВСА = 50 °.
Определите косинус угла между треугольником A B1C и плоскостью основания куба ABCDA1B1C1D1 со стороной 1.
Объяснение:
Нужно найти двугранный угол В₁АСВ.
В кубе все грани квадраты. Диагональ квадрата равна √(1²+1²)=√2 , половина диагонали 0,5√2. Пусть О-точка пересечения диагоналей основания.
Диагонали квадрата взаимно перпендикулярны , значит ОВ⊥АС. Тк. проекция ОВ⊥АС ,прямой лежащей в плоскости , то и наклонная В₁О⊥АС. Поэтому ∠В₁ОВ-линейный угол двугранного В₁АСВ.
ΔВВ₁О- прямоугольный , tg∠В₁ОВ=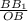
, tg∠В₁ОВ= 
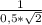=√2.
1+tg²∠В₁ОВ=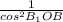
, 1+√2²=
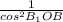,cos∠B₁OB=
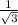, cos∠B₁OB=