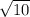Нарисуйте холм с горизонталей, проведённых через 20 м. Известно, что восточный склон более крутой, чем западный. Абсолютная высота — 72 м. Укажите с стрелки направление север — юг. НАПИШИТЕ в течении 5 минут тогда лучший ответ ваш
А) Пусть SO высота пирамиды, а KH — перпендикуляр, проведенный из K к плоскости ABC. Очевидно, что основание перпендикуляра H — проекция точки K, лежит на BO — проекции BS. Докажем, что M, H и С лежат на одной прямой. Пусть MC пересекает BO в точке T, и пусть N — середина AB. Запишем теорему Менелая для треугольника BNO и прямой CM: дробь, числитель — BM, знаменатель — MN умножить на дробь, числитель — NC, знаменатель — CO умножить на дробь, числитель — OT, знаменатель — TB = 1, тогда дробь, числитель — 2, знаменатель — 7 умножить на дробь, числитель — 3, знаменатель — 2 умножить на дробь, числитель — OT, знаменатель — TB = 1. Из последнего соотношения получаем: OT : TB = 7 : 3. Но OH : HB = SK : KB = 7 : 3. Значит, точки H и T совпадают. Следовательно, CM пересекает BO в точке H. Плоскость KMC содержит KH, которая перпендикулярна ABC, таким образом, плоскости KMC и ABC перпендикулярны. Поэтому плоскость α проходит через точку C. б) Заметим, что KH= дробь, числитель — 3, знаменатель — 10 SO= дробь, числитель — 3, знаменатель — 10 корень из { SA в степени 2 минус AO в степени 2 }= дробь, числитель — 6, знаменатель — 5 .
Вычислим CM при теоремы косинусов: CM в степени 2 =9 в степени 2 плюс 1 в степени 2 минус 2 умножить на 9 умножить на 1 умножить на косинус 60 в степени circ = 73. Поэтому площадь треугольника CKM равна S= дробь, числитель — 1, знаменатель — 2 умножить на дробь, числитель — 6, знаменатель — 5 умножить на корень из { 73}= дробь, числитель — 6 корень из { 73}, знаменатель — 10 . ответ: б) дробь, числитель — 6 корень из { 73}, знаменатель — 10 .
б) Заметим, что
KH= дробь, числитель — 3, знаменатель — 10 SO= дробь, числитель — 3, знаменатель — 10 корень из { SA в степени 2 минус AO в степени 2 }= дробь, числитель — 6, знаменатель — 5 .
Вычислим CM при теоремы косинусов:
CM в степени 2 =9 в степени 2 плюс 1 в степени 2 минус 2 умножить на 9 умножить на 1 умножить на косинус 60 в степени circ = 73.
Поэтому площадь треугольника CKM равна
S= дробь, числитель — 1, знаменатель — 2 умножить на дробь, числитель — 6, знаменатель — 5 умножить на корень из { 73}= дробь, числитель — 6 корень из { 73}, знаменатель — 10 .
ответ: б) дробь, числитель — 6 корень из { 73}, знаменатель — 10 .
1. Прямая ВC формула прямой у=(3-х)/7
Прямая АВ формула прямой у=2х-21
Прямая АС формула прямой у= -х-3
2. у=9-3х медиана АА1
у=1/3х-39/9 - медиана ВВ1
у= -0,5х-1 - медиана СС1
3. у(АА2)=7,1х-51,5
ВВ2 высота у=х-11
СС2 уравнение у= -0,5х-1
4. А3(5;-6) т пересечения медианы АА1 и высоты ВВ2
5.tg∠A=3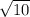
tg∠B=tg∠A
tg∠C=2/3/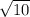
Объяснение:
1. Коэфициент при х - это (у-уо)/х т.В(10;-1)
для ВС (у-уо)/х=(-1+21)/10=2
2. АА1 - медиана Определим координаты А1(3; 0)
уравнение медианы АА1
у=9-3х
ВВ1 - медиана В1(1; -4)
у=1/3х-39/9
СС1 С1 (8; -5)
у= -0,5х-1
3.АА2 высота
А2 (7,2; -0,6)
у(АА2)=8,5/1,2х-61,8/1,2=7,1х-51,5
ВВ2 высота
координата В2=(4; -7)
у=х-11
СС2 тС2=С1 (8; -5)
у= -0,5х-1
5. tg∠A=CC1/AC1
Определяем модули векторов СС1 (12;-6) и АС1 (2;4)
tg∠A=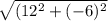 /
/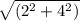 =3
=3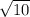
tg∠B=tg∠A
tg∠C=2*AC1/CC1=2*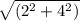 /
/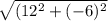 =2/3/
=2/3/