Найдите апофему правильной усечённой пятиугольной пирамиды, стороны оснований которой равны 6 и 10, а площадь боковой поверхности 280

Показать ответ

Ответ:

neleachibzii

19.06.2021 05:40

ответ: 7,5см

Объяснение: если диагональ тупого угла является его биссектрисой, то большее основание равно боковой стороне:

Обозначим вершины трапеции А В С Д а диагональ тупого угла ВД. Рассмотрим полученный ∆АВД. В нём АДВ=углу СВД как внутренние разносторонние, и так как АД- биссектриса, то угол АВД=углу СВД. Треугольник АВД-равнобедренный, поскольку его углы равны при основании и соответственно АВ=АД. Из этого следует, что меньшее основание ВС=6см, а большее основание АД и боковая сторона АВ=9см

Средняя линия трапеции это полусумма её оснований:

Ср.лин=(ВС+АД)/2=(6+9)/2=15/2=7,5см

Діагональ рівнобічної трапеції є бісектрисою тупого кута. Знайдіть середню лінію якщо менша основа і

0,0(0 оценок)

Ответ:

arturdadayan

27.02.2022 01:15

Формула объёма конуса: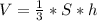 $V = \frac{1}{3}*S*h$ , где

S - площадь основания

h - высота конуса

Т.к. основанием конуса является круг, то

Формула площади круга: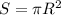 $S = \pi R^{2}$ , где

π - число пи

R - радиус круга

Как мы знаем радиус - половина диаметра ⇒ формула может выглядеть и так: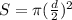 $S = \pi (\frac{d}{2}) ^{2}$

Получается формула объёма конуса становится такой: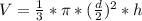 $V = \frac{1}{3}*\pi *(\frac{d}{2} )^{2} *h$

Теперь пусть d - диаметр нового конуса, тогда 2,5d - первоначальный диаметр конуса

V₁ - первоначальный объём конуса, а V₂ - новый объём конуса

Получается:

$V_{1} = \frac{1}{3}*\pi *(\frac{2,5d}{2} )^{2} *h = \frac{1}{3}*\pi *(\frac{5d}{4} )^{2} *h = \frac{1}{3}*\pi *\frac{25d^{2}}{16} *h$

$V_{2} = \frac{1}{3}*\pi *(\frac{d}{2} )^{2} *h = \frac{1}{3}*\pi *\frac{d^{2} }{4} *h$

Теперь ищем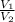 $\frac{V_{1} }{V_{2} }$

$\frac{V_{1} }{V_{2} } = \frac{\frac{1}{3}*\pi *\frac{25d^{2}}{16} *h}{\frac{1}{3}*\pi *\frac{d^{2} }{4} *h}$

$\frac{1}{3},\pi$ и h сокращаются, получается:

$\frac{V_{1} }{V_{2} } = \frac{\frac{25d^{2}}{16} }{ \frac{d^{2} }{4} } = \frac{25d^{2}}{16} : \frac{d^{2} }{4} = \frac{25d^{2}}{16} * \frac{4}{d^{2} } = \frac{25}{4} = 6 \frac{1}{4} = 6,25$