1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L = = 2 ≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So = a²/4=4. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3, площадь основания So=a²=36, объём V=Soh/3=36≈ 95,25 ≈ 95 см²
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L =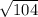
= 2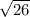
≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So =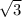
a²/4=4
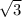. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6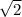
, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3
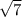, площадь основания So=a²=36, объём V=Soh/3=36
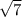≈ 95,25 ≈ 95 см²
Найдите площади боковой и полной поверхности правильной треугольной пирамиды со стороной основания 4 см и боковым ребром 6 см.
Объяснение:
АВСМ-правильная треугольная пирамида, АВС-основание, МА=6см, АС=4 см.
1)S(полн.пр.пир.)=S(осн)+S(бок) ;
S(бок)=1/2*Р(осн)*а, а-апофема,
S(осн)=S(прав. треуг)=(а²√3)/4.
2) S(осн)=(4²√3)/4= 4√3 (см²) ;
3)Пусть ВК⊥АС, тогда ВК-медиана ,т.к треугольник правильный ⇒
АК=2 см.
Т.к. ВК⊥АС, то МК⊥АС по т. о трех перпендикулярах (МО-высота прирамиды). Тогда ΔАМК-прямоугольный, по т. Пифагора
МК=√(АМ²-АК²) , МК=√(36-4)=√32=4√2 (см).
4) Р( осн.)=4*3=12(см) ,
S(бок)=1/2*12*4√2=24√2 (см²)
5)S(полн.пр.пир.)=4√3+24√2 (см²)