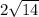Найдите координаты точек симметричных точке В(2:1) относительно: а) оси Ох: в) оси Оy; с) начала координат

Найдите координаты точек симметричных точке В(2:1) относительно: а) оси Ох: в) оси Оy; с) начала коо

Показать ответ

Ответ:

лулу36

08.12.2021 09:42

1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.

a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.

4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.

a₃ = R√3 ⇒ a₃ = 3√3 см

S(равностороннего треуг.)=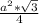 $\frac{a^{2}*\sqrt{3} }{4}$ ⇒ S(равн.треуг.)= 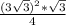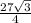$\frac{(3\sqrt{3})^{2}*\sqrt{3} }{4}$ = $\frac{27 \sqrt{3} }{4}$ (cм²)

5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.

Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .

160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.

((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )

6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.

a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.

Квадрат описан около окружности, значит сторона квадрата равна

a₄ =2r или a₄ =4см.

0,0(0 оценок)

Ответ:

Vafelka225

10.04.2021 13:30

Объяснение:

Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:

c^2 = a^2 + b^2 (^2 - вторая степень числа)

Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)

a^2 = c^2 - b^2

Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2

$a = \sqrt{c^2 - b^2}$