S полной поверхности параллелепипеда = 2 S основания + 4 S боковой грани S основания = S ромба = * на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
это равносторонний треугольник
2 диагональ из равностороннего треугольника со стороной a, и высотой a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами *a (половина 1 диагонали), гипотенуза = a.
По т.пифагора: (корень из 3)*a/2
2 диагональ (равна корень из 3)*a
площадь основания = (корень из 3)*a*a/2. найдем высоту. 45 град. угол между диагональю параллелепипеда и 2 диагональю ромба.
в треугольнике, образованном диагональю параллелепипеда диагональю ромба и боковой стороной параллелепипед один угол 45 град, второй = 90 град, то третий будет 180 - 45 - 90.
данный треугольник - равносторонний и высота равна диагонали ромба т.е. (корень из 3)*a. (в следствии)
Следовательно площадь боковой грани = a*(корень из 3)*a Итого П.П.П. = 2*(корень из 3)*a*a/2 + 4*a*(корень из 3)*a = 5*(корень из 3)*(a в квадрате) (формулой)
рассмотрим треугольники СВО и ОВД мы видим что СО = ОД по условию задачи , углы прямые (СОВ = ДОВ) сторона ОВ общая , значит треугольники СОВ и ДОВ равны по двум сторонам и углу между ними то есть по 1 признаку равенства треугольников . Рассмотрим треугольники АОС и АОД , АО- общая сторона , СО = ОД по условию задачи , а углы равные ( по свойству смежных углов и вертикальных углов) значит треугольники АОС = АОД по двум сторонам и углу между ними то есть тоже по 1 признаку равенства треугольников. Теперь если треугольник АОС = треугольнику АОД и треугольник СОВ = треугольнику ДОВ значит треугольники АВС и АВД равные
S полной поверхности параллелепипеда = 2 S основания + 4 S боковой грани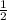 * на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
* на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
S основания = S ромба =
это равносторонний треугольник
2 диагональ из равностороннего треугольника со стороной a, и высотой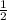 a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами
a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами 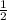 *a (половина 1 диагонали), гипотенуза = a.
*a (половина 1 диагонали), гипотенуза = a.
По т.пифагора: (корень из 3)*a/2
2 диагональ (равна корень из 3)*a
площадь основания = (корень из 3)*a*a/2.
найдем высоту. 45 град. угол между диагональю параллелепипеда и 2 диагональю ромба.
в треугольнике, образованном диагональю параллелепипеда диагональю ромба и боковой стороной параллелепипед один угол 45 град, второй = 90 град, то третий будет 180 - 45 - 90.
данный треугольник - равносторонний и высота равна диагонали ромба т.е. (корень из 3)*a. (в следствии)
Следовательно площадь боковой грани = a*(корень из 3)*a
Итого П.П.П. = 2*(корень из 3)*a*a/2 + 4*a*(корень из 3)*a = 5*(корень из 3)*(a в квадрате) (формулой)
рассмотрим треугольники СВО и ОВД мы видим что СО = ОД по условию задачи , углы прямые (СОВ = ДОВ) сторона ОВ общая , значит треугольники СОВ и ДОВ равны по двум сторонам и углу между ними то есть по 1 признаку равенства треугольников . Рассмотрим треугольники АОС и АОД , АО- общая сторона , СО = ОД по условию задачи , а углы равные ( по свойству смежных углов и вертикальных углов) значит треугольники АОС = АОД по двум сторонам и углу между ними то есть тоже по 1 признаку равенства треугольников. Теперь если треугольник АОС = треугольнику АОД и треугольник СОВ = треугольнику ДОВ значит треугольники АВС и АВД равные