Решение: я за максимальную простоту вычислений и применения самых известных формул. Так как площадь одной клетки 1ед²( должна быть в кв!, т.к. это площадь), то и длина стороны квадратика- 1 единица. теперь достроим этот квадратик до прямоугольника со сторонами 3 на 4 единицы. Искомая площадь= Ето разность площади четырёхугольника и двух прямоугольних треугольников. Меньший треугольник с катетами: 1 и 2 единицы, а большего треугольника 2 и 3 единицы. теперь запишем это всё математически и решим:
ответ : 8
Решение: я за максимальную простоту вычислений и применения самых известных формул. Так как площадь одной клетки 1ед²( должна быть в кв!, т.к. это площадь), то и длина стороны квадратика- 1 единица. теперь достроим этот квадратик до прямоугольника со сторонами 3 на 4 единицы. Искомая площадь= Ето разность площади четырёхугольника и двух прямоугольних треугольников. Меньший треугольник с катетами: 1 и 2 единицы, а большего треугольника 2 и 3 единицы. теперь запишем это всё математически и решим:
S= Sпр-Sтр мал-Sтр бол=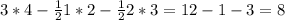 ( ед²
( ед²
1.Если хорда равна радиусу окружности, то она стягивает дугу в 60°.
следовательно:
Дуга СВ = 60°, тогда центральный угол СОВ = 60°.
По теореме о сумме смежных углов :
<СОА + <СОВ = 180°
<СОА = 120°
ответ: 120°.
2.Проведем радиусы в точки касания.
Радиусы, проведенные в точки касания, перпендикулярны касательной.
Тоесть угол АСО = 90°
ОС - радиус, а радиус в два раза меньше диаметра. Так как ОА = диаметру (по условию), то и ОА = 2*ОС.
Если катет равен половине гипотенузы, то противолежащий этому катету равен 30°.
То есть угол ОАС = 30°
Рассмотрим треугольник АВС.
Отрезки ксательных, проведённых из одной точки равны, тоесть - АВ = АС, тогда треугольник АВС - равнобедренный.
АО - биссектриса <АВС (также свойство касательных), тогда АО перпендикулярен ВС.
Рассмотрим треугольник МАС - прямоугольный.
Против угла в 30° лежит катет, равный половине гипотенузы. То есть МС = ½АС = 2,5.
МС = ½ВС (свойство биссектрисы равнобедренного треугольника, проведенной к основанию)
МС = ½*ВС => ВС = 5.
ответ: 5.