Найдите площадь круга, ограниченного окружностью, описанной около правильного треугольника, если площадь треугольника равна найдите площадь круга огрниченого окружностью описанной около правильного треугольника если площадь треугольника равна 12√3 см2
16 см^2.
Объяснение:
Формула площади правильного треугольника через сторону: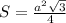 , откуда
, откуда 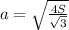 .
.
Формула нахождения радиуса описанной около правильного треугольника окружности: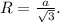 Тогда площадь круга, ограниченного окружностью с таким радиусом, будет вычисляться как
Тогда площадь круга, ограниченного окружностью с таким радиусом, будет вычисляться как 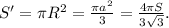
Вычисляем: