Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.
⇒ x + 0,2x = 180
1,2x = 180
x = 180 ÷ 1,2
x = 150° (внутренний угол выпуклого многоугольника)
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 150° × n
Отсюда выходит что:
150n = 180(n-2)
Находим n:
150n = 180n - 360
180n - 150n = 360
30n = 360
n = 360 ÷ 30
n = 12 (количество сторон правильного многоугольника)
Задание 3
а) ответ: Площадь многоугольника = 64 см².
Объяснение:
Правильный многоугольник, в котором n = 4 это КВАДРАТ.
Диаметр окружности d = 2r, где r - радиус
Известно что сторона квадрата a равна диаметру d вписанной в него окружности
⇒ d = a = 2r = 2×4 = 8 cm.
Площадь квадрата = a² = 8² = 64 cm²
б) ответ: Радиус вписанной окружности см.
Объяснение:
Известно что сторона квадрата , где r - радиус вписанной окружности.
Так же известно что сторона квадрата , где R - радиус описанной окружности ⇒
(радиус вписанной окружности)
в) ответ: Периметр многоугольника = 16 см.
Объяснение:
Известно что сторона квадрата , где R - радиус описанной окружности
⇒
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.
1. Сумма углов четырехугольника - 360 градусов. Четвертый угол равен разности 360 и суммы всех остальных углов. 360 - 41 - 21 - 27 = 271 градус. Но в выпуклом четырехугольнике каждый из углов меньше 180, так что наверное задание неправильно составлено
2. По свойству параллелограмма его противоположные стороны равны. обозначим сторону из первой пары за a, из второй за b. Составим уравнение:
a = 30b
2a + 2b = 62
Заменим в уравнении периметра a на 30b
60b + 2b = 62
62b = 62
b = 1
a = 30 * 1 = 30
3. В параллелограмме, которым является прямоугольник диагонали делятся своим пересечением напополам. Тогда ΔPEF равнобедренный с основанием PF. ∠EPF = ∠EFP = 26 ∠PEF = 180 - 26 - 26 = 128(по сумме углов треугольника) ∠PEK смежный с ∠PEF, а ∠KED вертикальный с ним. Тогда по свойствам смежных и вертикальных углов ∠PEK = 180 - 128 = 52, ∠KED = ∠PEF = 128
4. По свойству ромба диагонали делят его углы напополам. Значит, образуя с его стороной угол в 75, весь угло равен 150. Противоположные углы в ромбе равны, значит второй угол равен 180 - 150 = 30.
5. Обозначим первую сторон трапеции за a, вторую за b, третью за c, четвертую за d. Составим уравнения:
Задание 1
ответ: Да, существует. Это правильный 8-ми угольник (см. картинку №1).
Объяснение:
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 135° × n
Отсюда выходит что:
135n = 180(n-2)
Находим n:
135n = 180n - 360
180n - 135n = 360
45n = 360
n = 360 ÷ 45
n = 8 (количество сторон правильного многоугольника)
Задание 2
ответ: Количество сторон правильного многоугольника = 12 (см. картинку №2).
Объяснение:
Пускай внутренний угол правильного многоугольника = x°
⇒ смежный с ним угол = 0,2x°
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.
⇒ x + 0,2x = 180
1,2x = 180
x = 180 ÷ 1,2
x = 150° (внутренний угол выпуклого многоугольника)
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 150° × n
Отсюда выходит что:
150n = 180(n-2)
Находим n:
150n = 180n - 360
180n - 150n = 360
30n = 360
n = 360 ÷ 30
n = 12 (количество сторон правильного многоугольника)
Задание 3
а) ответ: Площадь многоугольника = 64 см².
Объяснение:
Правильный многоугольник, в котором n = 4 это КВАДРАТ.
Диаметр окружности d = 2r, где r - радиус
Известно что сторона квадрата a равна диаметру d вписанной в него окружности
⇒ d = a = 2r = 2×4 = 8 cm.
Площадь квадрата = a² = 8² = 64 cm²
б) ответ: Радиус вписанной окружности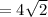 см.
см.
Объяснение:
Известно что сторона квадрата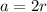 , где r - радиус вписанной окружности.
, где r - радиус вписанной окружности.
Так же известно что сторона квадрата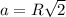 , где R - радиус описанной окружности ⇒
, где R - радиус описанной окружности ⇒
в) ответ: Периметр многоугольника = 16 см.
Объяснение:
Известно что сторона квадрата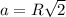 , где R - радиус описанной окружности
, где R - радиус описанной окружности
⇒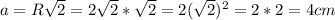
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.
⇒ P = 4 × 4 = 16 cm
1. Сумма углов четырехугольника - 360 градусов. Четвертый угол равен разности 360 и суммы всех остальных углов. 360 - 41 - 21 - 27 = 271 градус. Но в выпуклом четырехугольнике каждый из углов меньше 180, так что наверное задание неправильно составлено
2. По свойству параллелограмма его противоположные стороны равны. обозначим сторону из первой пары за a, из второй за b. Составим уравнение:
a = 30b
2a + 2b = 62
Заменим в уравнении периметра a на 30b
60b + 2b = 62
62b = 62
b = 1
a = 30 * 1 = 30
3. В параллелограмме, которым является прямоугольник диагонали делятся своим пересечением напополам. Тогда ΔPEF равнобедренный с основанием PF. ∠EPF = ∠EFP = 26 ∠PEF = 180 - 26 - 26 = 128(по сумме углов треугольника) ∠PEK смежный с ∠PEF, а ∠KED вертикальный с ним. Тогда по свойствам смежных и вертикальных углов ∠PEK = 180 - 128 = 52, ∠KED = ∠PEF = 128
4. По свойству ромба диагонали делят его углы напополам. Значит, образуя с его стороной угол в 75, весь угло равен 150. Противоположные углы в ромбе равны, значит второй угол равен 180 - 150 = 30.
5. Обозначим первую сторон трапеции за a, вторую за b, третью за c, четвертую за d. Составим уравнения:
a + b + c + d = 370
a = b + 96
b + 96 + b + 89 + 95 = 370
2b = 90
b = 45 см
a = 45 + 96 = 141 см