Найдите площадь треугольника, две стороны которого равны 3см и 8см, а угол между ними равен а) 30° б) 45° в) 60° г) 90°.

Показать ответ

Ответ:

Иленьк

16.02.2020 14:52

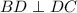Дано: ABCD - параллелограмм. $BK\perp AD$ , AK=64 см, KD=225 cм, $BD\perp DC$ .

Найти: BD

Решение: Треугольник АВD является прямоугольным, так как BD перпендикулярно DC. A DC||AB. Значит BD является секущей при параллельных АВ и CD. Поэтому

$\angle ABD=\angle BDC=90^\circ$

Есть такое свойство в прямоугольном треугольнике, что высота, проведенная к гипотенузе, является средним геометрическим отрезков, на которое делит высота гипотенузу.

$BK=\sqrt{AK*KD}=\sqrt{64*225}=\sqrt{8^2*15^2}=8*15=120$

BK=120 см.

Теперь по теореме Пифагора BD - гипотенуза треугольника BKD.

BD^2=BK^2+KD^2

$BD=\sqrt{BK^2+KD^2}=\sqrt{120^2+225^2}=$

$=\sqrt{(3*2^3*5)^2+(3^2*5^2)^2}=\sqrt{3^2*2^6*5^2+3^4*5^4}=$

$\sqrt{3^2*5^2*(2^6+3^2*5^2)}=3*5*\sqrt{2^6+15^2}=15\sqrt{64+225}=$

$=15\sqrt{289}=15*17=255$

ответ: BD=255 cм.

Впараллелограмме abcd высота, опущенная из вершины тупого угла в делит сторону аd на отрезки ак=64 с

0,0(0 оценок)

Ответ:

Danlika

08.04.2022 03:30

Заданная сторона АВ, О - точка пересечения медиан, S - площадь треугольника АВС.

Тогда площадь треугольника АОВ равна S/3,

а стороны АО = 18*(2/3) = 12, ВО = 24*(2/3) = 16, АВ = 20.

Очевидно, что АОВ - "египетский" треугольник (то есть прямоугольный треугольник, подобный треугольнику со сторонами 3,4,5, коэффициент подобия равен 4), поэтому его площадь равна 12*16/2 = 96, а площадь АВС S = 96*3 = 288

Что вы там у Гоши68 нашли неправильного? Все он верно сделал, просто написал без пояснений. Другое дело, что можно было бы заметить, что АОВ - прямоугольный треугольник, но и без этого все равно решение верное.

Вообще-то, я хочу пару слов сказать тут тем, кто серьезно готовится к экзаменам. Если вы применяете такую вещь, как формула Герона - вы должны быть готовы на ходу её вывести, если преподаватель потребует. И не только её, а еще и кучу сопутствующих формул вроде малоизвестной теоремы тангенсов ... А это намного сложнее и длинее, чем эта детская задачка.

0,0(0 оценок)

Популярные вопросы: Геометрия