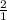АВ=ВС, т.к. треугольник равнобедренный, а АС - основание. ВК=2, АК=8, тогда, АВ=10. Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов. АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16. В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6. Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.
на сторонах bc и cd параллелограмма abcd отметили соответственно точки F и E так , что BF:FC= 0,5 , DE: EC=0,75.Прямые FD и AE пересекаются в точке M.Найдите отношение FM:MD
Объяснение:
BF:FC= 1/2 , DE: EC=3/4.
Пусть ВС=а, DC=в. Тогда FC= a
1) ΔFMY ≈ΔDMA по двум вертикальным углам и накрест лежащем при ВС║AD, AY-секущая : ∠FMY=DMA , ∠FYM=∠DAM.
В подобных треугольниках сходственные стороны пропорциональны или .
2) ΔCEY ≈ΔDEA по двум вертикальным углам и накрест лежащем :при ВС║AD, AY-секущая : ∠СEY=DEA , ∠CYE=∠EAD.
В подобных треугольниках сходственные стороны пропорциональны или CY=
ВК=2, АК=8, тогда, АВ=10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов.
АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16.
В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6.
Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.
на сторонах bc и cd параллелограмма abcd отметили соответственно точки F и E так , что BF:FC= 0,5 , DE: EC=0,75.Прямые FD и AE пересекаются в точке M.Найдите отношение FM:MD
Объяснение:
BF:FC= 1/2 , DE: EC=3/4.
Пусть ВС=а, DC=в. Тогда FC=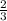 a
a
1) ΔFMY ≈ΔDMA по двум вертикальным углам и накрест лежащем при ВС║AD, AY-секущая : ∠FMY=DMA , ∠FYM=∠DAM.
В подобных треугольниках сходственные стороны пропорциональны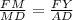 или
или 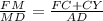 .
.
2) ΔCEY ≈ΔDEA по двум вертикальным углам и накрест лежащем :при ВС║AD, AY-секущая : ∠СEY=DEA , ∠CYE=∠EAD.
В подобных треугольниках сходственные стороны пропорциональны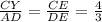 или CY=
или CY=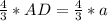
3)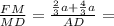
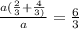 =
=