Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
, тогда а= .
По т. Пифагора а²+b²=(3+4)² ,( )²+b²=49 ,
+b²=49 , 9b²+16b²=49*16 , b²= , b== 5,6 (см)
a= =4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
Найти площадь квадрата, если радиус круга R, описанного вокруг него, равен 6√2 см
а) 72 см² б) 144 см² в) 36 см² г) 18 см²
- - - - - - - - - - -
"Решение " : S= d*d/2 , где d - диагональ квадрата и d =2R
( R - радиус круга , описанного вокруг этого квадрата)
S = 2R² =2*(6√2 см)² =2*6*(√2)² см² =2*36*2 см² = 1 44 см² .
ответ : 1 44 см² → б)
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Пусть a длина стороны квадрата
S = a²
R = d /2 , d=√(a²+a²) = a √2
R = a √2 /2 ⇔ a = 2R/√2
Окончательно : S = a² =(2R/√2)² = 4R²/2 = 2R² =2*(6√2 см)² = 144 см².
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
По т. Пифагора а²+b²=(3+4)² ,(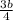
)²+b²=49 ,
a=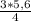
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."