Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=.
Гомотетия-преобразование плоскости или пространства, при котором каждой точке М ставится в соответствие точка М', лежащая на ОМ, О - фиксированная точка, причем отношение ОМ' : ОМ = k (коэффициент гомотетии) одно и то же для всех точек М, отличных от О Центр гомотетии лежит на отрезке с указанными координатами и делит отрезок в отношении Коэффициент - числовой множитель при буквенном выражении, известный множитель при той или иной степени неизвестного или постоянный множитель при переменной величине.
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=
.
ΔАОК- прямоугольный ,
cos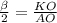
, KO=R*cos
;
sin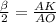
,AK=R*sin
,AB=α2Rsin
.
ΔSKO прямоугольный ,cos α=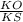
, KS=R*cos
/cosα.
S=0,5*AB*SK ,S=0,5*2R*sin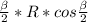
/ cosα,
S=0,5*R²*sinβ/cosα=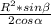
Центр гомотетии лежит на отрезке с указанными координатами и делит отрезок в отношении
Коэффициент - числовой множитель при буквенном выражении, известный множитель при той или иной степени неизвестного или постоянный множитель при переменной величине.