5. Пользуемся ответами от 3 и 4 задания.Сумма периметров треугольников АВС и DEF равна 16 см (7 см+9 см). Я не знаю, там нужно писать единицы измерения или нет.
На сколько я понял требуется решить только первую задачу.
Дана трапеция ABCD, AB=CD=7√2 см; AC⊥BD.
Найти радиус описанной около ABCD.
Пусть AC∩BD=F и пусть ∠FAB=α.
Вокруг равнобедренной трапеции всегда можно описать окружность!
ΔABD=ΔDCA по двум сторонам и углу между ними (AB=DC; AD - общая; ∠BAD=∠CDA), поэтому ∠ADB=∠DAC, как углы лежащий напротив равных сторон в равных треугольниках.
В ΔAFD:
∠AFD=90°; ∠FAD=∠FDA=(180°-∠AFD):2=90°:2=45°. Таким образом ΔAFD - равнобедренный прямоугольны, AF=DF.
В прямоугольном ΔAFB:
AF=AB·cosα=7√2·cosα см
BF=AB·sinα=7√2·sinα см
В ΔABD:
BD=BF+FD=BF+AF=7√2·(sinα+cosα) см
∠BAD=α+45°
Вокруг ΔABD описана таже окружность, что и вокруг трапеции.
Написала на картинке.
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания.Сумма периметров треугольников АВС и DEF равна 16 см (7 см+9 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 16 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 16 см
PK+KL+LM+MN+NR+PR < 8 см.
Это нам и нужно было доказать!
На сколько я понял требуется решить только первую задачу.
Дана трапеция ABCD, AB=CD=7√2 см; AC⊥BD.
Найти радиус описанной около ABCD.
Пусть AC∩BD=F и пусть ∠FAB=α.
Вокруг равнобедренной трапеции всегда можно описать окружность!
ΔABD=ΔDCA по двум сторонам и углу между ними (AB=DC; AD - общая; ∠BAD=∠CDA), поэтому ∠ADB=∠DAC, как углы лежащий напротив равных сторон в равных треугольниках.
В ΔAFD:
∠AFD=90°; ∠FAD=∠FDA=(180°-∠AFD):2=90°:2=45°. Таким образом ΔAFD - равнобедренный прямоугольны, AF=DF.
В прямоугольном ΔAFB:
AF=AB·cosα=7√2·cosα см
BF=AB·sinα=7√2·sinα см
В ΔABD:
BD=BF+FD=BF+AF=7√2·(sinα+cosα) см
∠BAD=α+45°
Вокруг ΔABD описана таже окружность, что и вокруг трапеции.
По теореме синусов: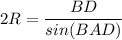
, где R - радиус описанной.
ответ: 7 см.