В треугольнике СDE угол СDE = 90 градусов, т.к. DE перп. DC по условию, тогда ЕС - гипотенуза. Проведём из точки D к гипотенузе медиану DM, медиана из вершины прямого угла равна половине гипотенузы, тогда DM = EC/2=1. Треугольник DMC - равнобедренный, тогда углы MDC и MCD равны, но СD - биссектриса, значит углы ВСD и DCM также равны, т.е. углы MDC и BCD равны, значит медиана DM параллельна стороне ВС, т.к. равны накрест лежащие углы при секущей DС, тогда углы ADM и АВС равны как соответственные углы при параллельных прямых, тогда треугольники ADM и АВС подобны по 2 углам, значит AD/DM=AB/BC, но АВ=ВС, т.к. исходный треугольник равнобедренный, т.е. AD/DM=1, значит AD=DM=1.
Точка одинаково удалена от всех вершин прямоугольного треугольника на 1 см, а от плоскости этого треугольника на 0.5 см найдите медиану гипотезе этого треугольника
Объяснение:
1.Пусть КМ-медиана ΔAКB - равнобедренный, поэтому КM ⊥ AB по свойству медианы равнобедренного треугольника.
Пусть в ΔКCM проведем КO⊥ СМ. Тогда ОА=ОВ=ОС как проекции равных наклонных равный наклонные, поэтому ОА = ОВ= ОС = R, R - радиус описанной окружности около ΔАВС. Но центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы , поэтому точки М и О совпадают. ⇒
КM ⊥ ( АВС).
2)Т.к. М-середина АВ , то СМ-медиана к гипотенузе ΔАВС.
ΔАКМ-прямоугольный, АК=1 см, КМ=0,5 см, по т. Пифагора АМ=√(1²-0,5²)=√0,75= ( см).
Треугольник DMC - равнобедренный, тогда углы MDC и MCD равны, но СD - биссектриса, значит углы ВСD и DCM также равны, т.е. углы MDC и BCD равны, значит медиана DM параллельна стороне ВС, т.к. равны накрест лежащие углы при секущей DС, тогда углы ADM и АВС равны как соответственные углы при параллельных прямых, тогда треугольники ADM и АВС подобны по 2 углам, значит AD/DM=AB/BC, но АВ=ВС, т.к. исходный треугольник равнобедренный, т.е. AD/DM=1, значит AD=DM=1.
Интересная задачка напряг извилины.
Точка одинаково удалена от всех вершин прямоугольного треугольника на 1 см, а от плоскости этого треугольника на 0.5 см найдите медиану гипотезе этого треугольника
Объяснение:
1.Пусть КМ-медиана ΔAКB - равнобедренный, поэтому КM ⊥ AB по свойству медианы равнобедренного треугольника.
Пусть в ΔКCM проведем КO⊥ СМ. Тогда ОА=ОВ=ОС как проекции равных наклонных равный наклонные, поэтому ОА = ОВ= ОС = R, R - радиус описанной окружности около ΔАВС. Но центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы , поэтому точки М и О совпадают. ⇒
КM ⊥ ( АВС).
2)Т.к. М-середина АВ , то СМ-медиана к гипотенузе ΔАВС.
ΔАКМ-прямоугольный, АК=1 см, КМ=0,5 см, по т. Пифагора АМ=√(1²-0,5²)=√0,75=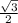
( см).
R=АМ=ВМ=СМ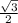, СМ=
см