Геометрия: Найти пары равных треугольников и доказать их равенство

Найти пары равных треугольников и доказать их равенство

Показать ответ

Ответ:

ravil863

14.06.2022 02:32

$S_{\triangle ABC} = \dfrac{3\sqrt{3} }{4}$ ; $P_{\triangle ABC} = 2\sqrt{3} + 3$

Объяснение:

Обозначим данный равнобедренный треугольник буквами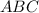 ABC .

$AB = \sqrt{3}$

$\angle ACB = 30^{\circ}$

==========================================================

Проведём высоту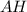 к основанию .

============================================================

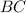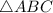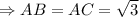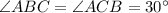Так как $\triangle ABC$ - равнобедренный $\Rightarrow AB = AC = \sqrt{3}$ и $\angle ABC = \angle ACB = 30^{\circ}$ , по свойству.

===========================================================

- высота, медиана, биссектриса $\triangle ABC$ , по свойству.

$\Rightarrow BH = HC.$

Рассмотрим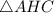 $\triangle AHC$ :

$\triangle AHC$ - прямоугольный, так как - высота.

Если угол прямоугольного треугольника равен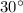 $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow AH = \dfrac{AC}{2} = \dfrac{\sqrt{3} }{2}$

Найдём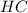 , по теореме Пифагора:

$HC^{2} = AC^{2} - AH^{2} = (\sqrt{3} )^{2} - (\dfrac{\sqrt{3} }{2} )^{2} = \dfrac{9}{4}$

$HC = \sqrt{\dfrac{9}{4} } = \dfrac{3}{2} = 1,5$

$S_{\triangle ABC} = CH \cdot AH = 1,5 \cdot \dfrac{\sqrt{3} }{2} = \dfrac{3\sqrt{3} }{4}$

==========================================================

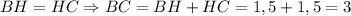
Так как $BH = HC \Rightarrow BC = BH + HC = 1,5 + 1,5 = 3$

$P_{\triangle ABC} = AB + BC + AC = \sqrt{3} + \sqrt{3} + 3 = 2\sqrt{3} + 3$

Решить равнобедренном треугольнике авс боковая сторона равна корень из 3 ,а угол при основании равен

0,0(0 оценок)

Ответ:

revati1

22.12.2021 00:48

Если вся диагональ = 6√3, то тогда половина диагонали = 3√3.
ABCD - ромб, значит диагонали пересекаются под прямым углом, тогда мы можем найти угол в одном из четырёх прямоугольных треугольников.
Рассмотрим треугольник BOC (угол BOC = 90°).
BC - 6см, BO - 3√3
Теперь можно найти синус угла BCO по противолежащему катету и гипотенузе:
3√3/6=sin3√2=60°
Т.к мы ищем углы ромба, то весь угол С = 120° (диагональ ромба делит угол пополам)
Угол С=А=120° (т.к ABCD - ромб)
Значит на два остальных угла приходится 120°, тогда два оставшихся угла = 60° каждый.
ответ: 120°, 120°, 60°, 60°.

Найдите углы ромба abcdесли его сторона равна 6 см а большая диогональ 6√3 см