В чем же особенность этих задач? Задачи на построение не просты. Не существует единого алгоритма для решения всех таких задач. Каждая из них по-своему уникальна, и каждая требует индивидуального подхо да для решения. Именно поэтому научиться решать задачи на построение чрезвычайно трудно, а, порой, практически невозможно.Но эти задачи дают уникальный материал для индивидуального творческого поиска путей решения с своей интуиции и подсознания. Любая ли задача решается с циркуля и линейки? Еще в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению.
∠AOB=90°
∠ABO=50°
∠BAO=40°
Объяснение:
Дано: ABCD - ромб
CD = 3 см
AC = 9 см
BD = 8 см
∠C = 80°
Найти: PΔ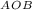 = ?
= ?
∠AOB=?
∠ABO=?
∠BAO=?
Решение: т.к ABCD - ромб, то у него все стороны равны ⇒ CD=BC=AB=AD=3 см
Диагонали ромба точкой пересечения делятся пополам: BO=OD=8/2=4 см; AO=OC=9/2=4,5 см
Противолежащие углы ромба равны ⇒ ∠C=∠A=80°, но т.к диагонали ромба являются биссектрисами его углов, то ∠OAD=∠BAO=80/2=40°
Диагонали ромба пересекаются под прямым углом ⇒ ∠AOB=90°
В ΔABO - прямоугольном, найдем ∠ABO. Сумма острых углов в прямоугольном треугольнике = 90°
∠ABO+∠BAO=90; ∠ABO=90-∠BAO; ∠ABO=90-40; ∠ABO=50°
Периметр - сумма длин всех сторон, тогда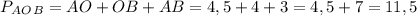 см
см
да для решения. Именно поэтому научиться решать задачи на построение чрезвычайно трудно, а, порой, практически невозможно.Но эти задачи дают уникальный материал для индивидуального творческого поиска путей решения с своей интуиции и подсознания.
Любая ли задача решается с циркуля и линейки? Еще в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению.