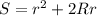Прямоугольный треугольник с катетами а и b и гипотенузой с. По теореме Пифагора: Зная, что гипотенуза равна двум радиусам описанной окружности, запишем: Добавим к обеим частям неравенства слагаемое 2аb и преобразуем его в правой части: Так как площадь прямоугольного треугольник равна половине произведения его катетов, то: Зная, что площадь треугольника равна половине произведения его периметр на радиус вписанной окружности, получим: Подставим вместо а+b и с известные выражения: Выполняем преобразования: Возведем обе части в квадрат: R² взаимно уничтожается, сокращаем на S: Домножаем на r: Площадь прямоугольного треугольника равна сумме удвоенного произведения радиусов вписанной и описанной окружности и квадрата радиуса вписанной окружности. (Или: площадь прямоугольного треугольника равна произведению радиуса вписанной окружности на сумму его же с диаметром описанной окружности) ответ: 2Rr+r²
Зная, что гипотенуза равна двум радиусам описанной окружности, запишем:
Добавим к обеим частям неравенства слагаемое 2аb и преобразуем его в правой части:
Так как площадь прямоугольного треугольник равна половине произведения его катетов, то:
Зная, что площадь треугольника равна половине произведения его периметр на радиус вписанной окружности, получим:
Подставим вместо а+b и с известные выражения:
Выполняем преобразования:
Возведем обе части в квадрат:
R² взаимно уничтожается, сокращаем на S:
Домножаем на r:
Площадь прямоугольного треугольника равна сумме удвоенного произведения радиусов вписанной и описанной окружности и квадрата радиуса вписанной окружности. (Или: площадь прямоугольного треугольника равна произведению радиуса вписанной окружности на сумму его же с диаметром описанной окружности)
ответ: 2Rr+r²
Для решения данной задачи воспользуемся такой теоремой:
Центр окружности описанной около прямоугольного треугольника, делит гипотенузу пополам.
Тогда имеем прямоугольный треугольник со сторонами:
Исходя из того что треугольник прямоугольный находим катеты:
Так как площадь прямоугольного треугольника равна: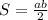
получаем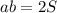
тогда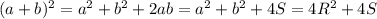
Получаем:
Зная, что площадь равна: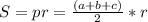
Получаем: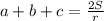
тогда получаем:
Прибавим с обеих сторон:
с обеих сторон:
т.к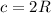 Получаем:
Получаем:
так как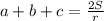
получаем:
Делим все на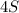 :
:
Откуда получаем:
ответ: