Сторона ромба с половинками диагоналей образует прямоугольный треугольник. Итак, имеем прямоугольный треугольник со сторонами 8 корней из 3 (гипотенуза) и 4 корня из 3 (один из катетов). Найдём второй катет: корень из (192 - 48) = 12.
Следовательно, вторая диагональ ромба равна 12 * 2 = 24.
Площадь ромба равна половине произведения его диагоналей.
Есть формула что сторона ромба(a) равна
Sромба=(1/2)*d1*d2=1/2*8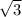 *24=96
*24=96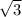
Сторона ромба с половинками диагоналей образует прямоугольный треугольник. Итак, имеем прямоугольный треугольник со сторонами 8 корней из 3 (гипотенуза) и 4 корня из 3 (один из катетов). Найдём второй катет: корень из (192 - 48) = 12.
Следовательно, вторая диагональ ромба равна 12 * 2 = 24.
Площадь ромба равна половине произведения его диагоналей.
S = (8 корней из 3 * 24) / 2 = 96 корней из 3.